题目内容
证明:任意一个反比例函数图象y=
关于y=±x轴对称.
| k |
| x |
考点:反比例函数图象的对称性
专题:证明题
分析:利用反比例函数图象上任意一点关于y=±x轴对称点还在反比例函数y=
图象上进行证明.
| k |
| x |
解答:证明:设P(a,b)为反比例函数图象y=
上任意一点,则ab=k,
点P关于直线y=x的对称点为(b,a),由于b•a=ab=k,所以点(b,a)在反比例函数y=
的图象上,即反比例函数图象y=
关于y=x轴对称;
点P关于直线y=-x的对称点为(-b,-a),由于-b•(-a)=ab=k,所以点(-b,-a)在反比例函数y=
的图象上,即反比例函数图象y=
关于y=-x轴对称,
即任意一个反比例函数图象y=
关于y=±x轴对称.
| k |
| x |
点P关于直线y=x的对称点为(b,a),由于b•a=ab=k,所以点(b,a)在反比例函数y=
| k |
| x |
| k |
| x |
点P关于直线y=-x的对称点为(-b,-a),由于-b•(-a)=ab=k,所以点(-b,-a)在反比例函数y=
| k |
| x |
| k |
| x |
即任意一个反比例函数图象y=
| k |
| x |
点评:本题考查了反比例函数图象的对称性:反比例函数图象既是轴对称图形又是中心对称图形,对称轴分别是:①二、四象限的角平分线y=-x;②一、三象限的角平分线y=x;对称中心是坐标原点.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列说法中正确的是( )
| A、两个数的差一定小于被减数 |
| B、若两数的差为0,则这两数必相等 |
| C、两个相反数相减必为0 |
| D、若两数的差为正数,则此两数都是正数 |
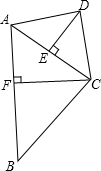 如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.