题目内容
 如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数.
如图,△ABC中,∠BAC=54°,∠BAC的外角平分线交直线BC于D,若AB+AC=BD,求∠ABC的度数.考点:等腰三角形的性质
专题:
分析:在BA的延长线上截取AE=AC,根据SAS可证△CAD≌△EAD,可得∠ACD=∠E,再根据等腰三角形的性质,三角形内角和定理,三角形外角的性质,可得方程组
,解方程即可求解.
|
解答: 解:在BA的延长线上截取AE=AC,
解:在BA的延长线上截取AE=AC,
∵AD是∠BAC的外角平分线,
∴∠CAD=∠EAD,
在△CAD与△EAD中,
,
∵△CAD≌△EAD(SAS),
∴∠ACD=∠E,
∵AB+AC=BD,
∴BE=BD,
∴∠E+
∠ABC=90°①,
又∵∠ACD=∠ABC+∠BAC,即∠E=∠ABC+54°②,
联立①②可得
,
解得∠ABC=24°.
故∠ABC的度数是24°.
 解:在BA的延长线上截取AE=AC,
解:在BA的延长线上截取AE=AC,∵AD是∠BAC的外角平分线,
∴∠CAD=∠EAD,
在△CAD与△EAD中,
|
∵△CAD≌△EAD(SAS),
∴∠ACD=∠E,
∵AB+AC=BD,
∴BE=BD,
∴∠E+
| 1 |
| 2 |
又∵∠ACD=∠ABC+∠BAC,即∠E=∠ABC+54°②,
联立①②可得
|
解得∠ABC=24°.
故∠ABC的度数是24°.
点评:本题考查了等腰三角形的性质:等腰三角形的两个底角相等,三角形全等的判定和性质,三角形内角和定理,三角形外角的性质,方程思想的运用,综合性较强,难度较大.

练习册系列答案
相关题目
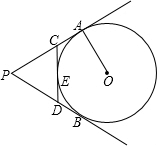 如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )
如图,PA,PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C,D.若△PCD的周长等于3,则PA的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
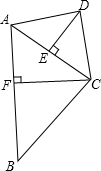 如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.