题目内容
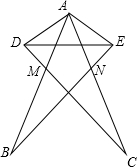 支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?
支撑高压电线的铁塔如图,其中AM=AN,∠DAB=∠EAC,AB=AC,问AD与AE能相等吗?为什么?考点:全等三角形的应用
专题:
分析:利用“边角边”证明△ABN和△ACM全等,根据全等三角形对应角相等可得∠B=∠C,再求出∠BAE=∠CAD,然后利用“角角边”证明△ABE和△ACD全等,根据全等三角形对应边相等证明即可.
解答:证明:AD=AE.
理由如下:在△ABN和△ACM中,
,
∴△ABN≌△ACM(SAS),
∴∠B=∠C,
∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
,
∴△ABE≌△ACD(AAS),
∴AD=AE.
理由如下:在△ABN和△ACM中,
|
∴△ABN≌△ACM(SAS),
∴∠B=∠C,
∵∠DAB=∠EAC,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠BAE=∠CAD,
在△ABE和△ACD中,
|
∴△ABE≌△ACD(AAS),
∴AD=AE.
点评:本题考查了全等三角形的应用,熟练掌握三角形全等的判断方法是解题的关键,难点在于需要二次证明三角形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
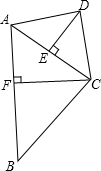 如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.