题目内容
17.小明进行射击训练,5次成绩分别为3环、4环、6环、8环,9环,则这5次成绩的方差为5.2.分析 根据平均数和方差公式计算即可.
解答 解:五次成绩的平均数为$\frac{1}{5}$(3+4+6+8+9)=6,
方差=$\frac{1}{5}$[(3-6)2+(4-6)2+(6-6)2+(8-6)2+(9-6)2]=5.2.
故答案为:5.2;
点评 本题考查平均数和方差的计算,关键是根据方差公式计算.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
5.如图,⊙O1的半径为1,正方形ABCD的边长为4,点O2为正方形ABCD的中心,O1O2⊥CD于点P,O1O2=5.现将⊙O1绕点P按顺时针方向旋转180°,则在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )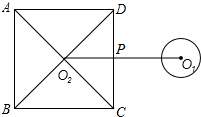

| A. | 1次 | B. | 2次 | C. | 3次 | D. | 4次 |
2.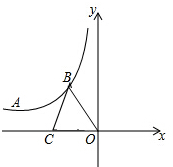 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
 如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )
如图,A点在y=$\frac{k}{x}$(x<0)的图象上,A点坐标为(-4,2),B是y=$\frac{k}{x}$(x<0)的图象上的任意一点,以B为圆心,BO长为半径画弧交x轴于C点,则△BCO面积为( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
9.某商场同时购进甲、乙两种商品共200件,其进价和售价如下表,
设其中甲种商品购进x件
(1)若该商场购进这200件商品恰好用去17900元,求购进甲、乙两种商品各多少件?
(2)若设该商场售完这200件商品的总利润为y元.
①求y与x的函数关系式;
②该商品计划最多投入18000元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调a元(50<a<70)出售,且限定商场最多购进120件,若商场保持同种商品的售价不变,请你根据以上信息及(2)中的条件,设计出使该商场获得最大利润的进货方案.
| 商品名称 | 甲 | 乙 |
| 进价(元/件) | 80 | 100 |
| 售价(元/件) | 160 | 240 |
(1)若该商场购进这200件商品恰好用去17900元,求购进甲、乙两种商品各多少件?
(2)若设该商场售完这200件商品的总利润为y元.
①求y与x的函数关系式;
②该商品计划最多投入18000元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
(3)实际进货时,生产厂家对甲种商品的出厂价下调a元(50<a<70)出售,且限定商场最多购进120件,若商场保持同种商品的售价不变,请你根据以上信息及(2)中的条件,设计出使该商场获得最大利润的进货方案.
6. 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
 寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )
寒假结束了,开学后小明对本校七年级部分同学寒假阅读总时间(结果保留整10小时)进行了抽样调查,所得数据整理后制作成如图所示的频数分布直方图.观察这个频数分布直方图,给出如下结论,正确的是( )| A. | 小明调查了100名同学 | |
| B. | 所得数据的众数是40小时 | |
| C. | 所得数据的中位数是30小时 | |
| D. | 全区有七年级学生6000名,寒假阅读总时间在20小时(含20小时)以上的约有5000名 |
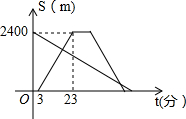 小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个
小红从劳动基地出发,步行返回学校,小军骑车从学校出发去劳动基地,在基地停留10分钟后,沿原路以原速返回,结果比小红早7分钟回到学校,若两人都是沿着同一路线行进,且两人与学校的距离s(米)和小红从劳动基地出发所用时间t(分)之间的函数关系如图所示,则下列说法中正确的结论有( )个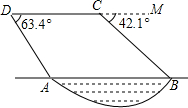 如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)
如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)