题目内容
8.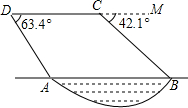 如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)
如图,某勘测飞机为了测量一湖泊两端A,B的距离,飞机在距离湖面垂直高度为90m点C处测得端点A的俯角为63.4°,然后沿着平行于AB的方向水平飞行了125米,在点D测得端点B的俯角为42.1°,求湖泊A、B两端的距离.(参考数据:tan63.4°≈2.00,sin63.4°≈0.89,cos63.4°≈0.45,tan42.1°≈0.90,sin42.1°≈0.67,cos42.1°≈0.74.)
分析 过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,利用三角函数求出AF的长,在Rt△BDF中,利用三角函数求出BE的长,进而可得AB的长.
解答  解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
解:如图,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F,
由题意可得∠ADC=63.4°,∠MDB=42.1°,CD=EF=125米,CE=DF=90米,
在Rt△ADF中,∠DAF=∠ACD=63.4°,
∵tan63.4°=$\frac{DF}{AF}$≈2.00,
∴AF=≈$\frac{90}{2.00}$=45米,
在Rt△BCE中,∠CBE=∠MDB=42.1°,
∵tan42.1°=$\frac{CE}{BE}$≈2.00,
∴BE=≈$\frac{90}{0.90}$=100米,
∴AB=EF-AF+BE=125-45+100=180米.
答:湖泊A、B两端的距离为180米.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列计算正确的是( )
| A. | (-2a2)3=8a6 | B. | a3÷a2=a | C. | 2a2+a2=3a4 | D. | (a-b)2=a2-b2 |
19.某天的最高气温是11℃,最低气温是-1℃,则这一天的最高气温与最低气温的差是( )
| A. | 2℃ | B. | -2℃ | C. | 12℃ | D. | -12℃ |
 一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$.
一名儿童行走在如图所示的地板上,当他随意停下时,最终停在阴影部分的概率是$\frac{1}{3}$.
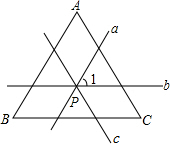 如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.
如图,P为△ABC内任意一点,过点P分别画a∥AB,b∥BC,c∥AC.那么只要再给出∠A、∠B、∠C三个角中哪一个角的度数,即可求得∠1的度数?试说明你的理由.