题目内容
甲、乙两门大炮在相同的条件下向同一目标各发射50发炮弹,炮弹落点情况如下表:
(1)已知
乙=4,求甲大炮所发射的炮弹落点与目标距离的平均数;
(2)已知S甲2=22,求乙大炮的方差,并指出哪门大炮射击的稳定性好?
| 炮弹落点与目标距离∕m | 20 | 15 | 10 | 5 | 0 |
| 甲炮发射的炮弹个数 | 0 | 3 | 9 | 13 | 25 |
| 乙炮发射的炮弹个数 | 1 | 5 | 9 | 3 | 32 |
. |
| x |
(2)已知S甲2=22,求乙大炮的方差,并指出哪门大炮射击的稳定性好?
考点:方差,加权平均数
专题:
分析:(1)根据平均数的计算公式先列出算式,再进行计算即可;
(2)根据方差公式先求出乙的方差,再与甲的方差进行比较,即可得出答案.
(2)根据方差公式先求出乙的方差,再与甲的方差进行比较,即可得出答案.
解答:解:(1)根据题意得:
(15×3+10×9+5×13)÷50=4(m),
答:甲大炮所发射的炮弹落点与目标距离的平均数是4m;
(2)根据题意得:
S乙2=
[(20-4)2+5×(15-4)2+9×(10-4)2+3×(5-4)2+32×(0-4)2]=34,
∵S甲2=22,S乙2=34,
∴S2甲<S2乙,
∴甲大炮射击的稳定性好.
(15×3+10×9+5×13)÷50=4(m),
答:甲大炮所发射的炮弹落点与目标距离的平均数是4m;
(2)根据题意得:
S乙2=
| 1 |
| 50 |
∵S甲2=22,S乙2=34,
∴S2甲<S2乙,
∴甲大炮射击的稳定性好.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
永辉超市同时售出两台冷暖空调,每台均卖990元,按成本计算,其中一台盈利10%,另一台亏本10%,则出售这两台空调永辉超市( )
| A、不赔不赚 | B、赚20元 |
| C、亏20元 | D、赚90元 |
 如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积.
如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积.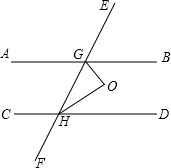 如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.
如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.
 如图,这是某市部分简图,为了确定各建筑物的位置:
如图,这是某市部分简图,为了确定各建筑物的位置: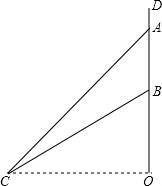 如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可)
如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可)