题目内容
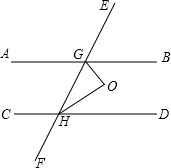 如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.
如图:AB∥CD,GO和HO分别是∠BGH和∠GHD的角平分线.你能算出∠GOH的度数吗?如果作OP⊥AB,OQ⊥CD,OR⊥EF,你能找到图中的全等三角形吗?说明理由.考点:全等三角形的判定,角平分线的性质
专题:
分析:根据两直线平行同旁内角互补可得∠BGH+∠DHG=180°,再由角平分线的定义不难推出∠MGH+∠MNG=90°,即得到GM与HM垂直.根据两直线平行以及三角形全等的概念可以得到答案.
解答:解:∵AB∥CD,
∴∠BGH+∠DHG=180°,
∵∠BGH和∠DHG的平分线交于点M,
∴∠BGM=∠MGH,∠GHM=∠MHD,
∴∠MGH+∠MHG=90°.
∴∠GOH=90°,
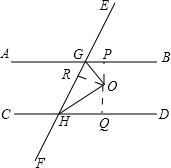
∵OP⊥AB,OQ⊥CD,OR⊥EF,GO和HO分别是∠BGH和∠GHD的角平分线.
∴OP=OR=OQ,
可以得到:△GPO和△GRO全等,△HRO和△HQO全等.
∴∠BGH+∠DHG=180°,
∵∠BGH和∠DHG的平分线交于点M,
∴∠BGM=∠MGH,∠GHM=∠MHD,
∴∠MGH+∠MHG=90°.
∴∠GOH=90°,
∵OP⊥AB,OQ⊥CD,OR⊥EF,GO和HO分别是∠BGH和∠GHD的角平分线.
∴OP=OR=OQ,
可以得到:△GPO和△GRO全等,△HRO和△HQO全等.

点评:此题主要考查学生对平行线的性质及角平分线的定义的综合运用能力.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
下列运算正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,为解决A、B、C、D四个村庄的用水问题,准备修建一个蓄水池,使蓄水池与四个村庄的距离的和最小.请画出蓄水池H的位置,并说明理由.
如图,为解决A、B、C、D四个村庄的用水问题,准备修建一个蓄水池,使蓄水池与四个村庄的距离的和最小.请画出蓄水池H的位置,并说明理由.