题目内容
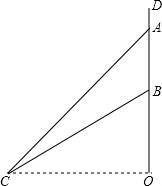 如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可)
如图,水渠边有一颗大木瓜树,树干DO(不计粗细)上有两个木瓜A、B(不计大小),树干垂直于地面,量得AB=2米,在水渠的对面与O处于同一水平面的C处测得木瓜A的仰角为45°、木瓜B的仰角为30°,求C处到树干DO的距离CO.(保留根号即可)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:设OC=x,在Rt△AOC中,由于∠ACO=45°,故OA=x,在Rt△BOC中,由于∠BCO=30°,故OB=OC•tan30°=
x,再根据AB=OA-OB=2即可得出结论.
| ||
| 3 |
解答:解:设OC=x,
在Rt△AOC中,
∵∠ACO=45°,
∴OA=OC=x,
在Rt△BOC中,
∵∠BCO=30°,
∴OB=OC•tan30°=
x,
∵AB=OA-OB=x-
x=2,
解得x=3+
.
∴OC=3+
(米).
答:C处到树干DO的距离CO约为(3+
)米.
在Rt△AOC中,
∵∠ACO=45°,
∴OA=OC=x,
在Rt△BOC中,
∵∠BCO=30°,
∴OB=OC•tan30°=
| ||
| 3 |
∵AB=OA-OB=x-
| ||
| 3 |
解得x=3+
| 3 |
∴OC=3+
| 3 |
答:C处到树干DO的距离CO约为(3+
| 3 |
点评:本题考查的是解直角三角形的应用-仰角俯角问题,先设出OC的长,利用锐角三角函数的定义及直角三角形的性质用x表示出OA、OB的长是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
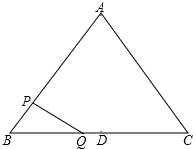 如图,在△ABC中,AB=AC=10,cosB=
如图,在△ABC中,AB=AC=10,cosB=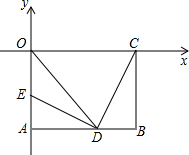 已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的负半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.
已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的负半轴上,OC在x轴的正半轴上,OA=2,OC=3.过原点O作∠AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E. 如图是由5个边长为1的小正方形拼成的,将这个图形分成三块(在图中画出),使由这三块可拼成一个正方形.
如图是由5个边长为1的小正方形拼成的,将这个图形分成三块(在图中画出),使由这三块可拼成一个正方形.