题目内容
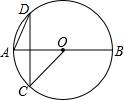如图，AB是⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=70°，则∠BOC=（ ）| A、70° | B、130° |
| C、140° | D、160° |
考点：圆周角定理,垂径定理
专题：
分析：由CD⊥AB，∠DAB=70°，可求得∠D的度数，又由圆周角定理，即可求得∠AOC的度数，继而求得答案．
解答：解：∵CD⊥AB．∠DAB=70°，
∴∠ADC=90°-∠DAB=20°，
∴∠AOC=2∠ADC=40°，
∴∠BOC=180°-∠AOC=140°．
故选：C．
∴∠ADC=90°-∠DAB=20°，
∴∠AOC=2∠ADC=40°，
∴∠BOC=180°-∠AOC=140°．
故选：C．
点评：此题考查了圆周角定理以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
已知AO⊥BO，DO⊥CO，∠AOD=4∠BOC，则∠AOD的度数为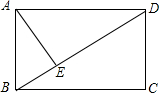
如图，在矩形ABCD中，AE⊥BD，垂足为E，BE=2，ED=6，求矩形ABCD的周长．
如图，已知∠1=∠2，∠A=∠D，求证：∠C=∠F．
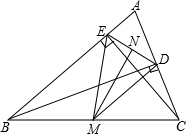如图，在△ABC中，BD⊥AC于D，CE⊥AB于E，点M、N分别是BC、DE的中点，连接ME、MD．点P是线段AB的黄金分割点（PA＞PB），则下列结论正确的有（ ）
①PA2=PB•AB；②
=
；③
=
．
①PA2=PB•AB；②
| PB |
| PA |
| PA |
| PB |
| PB |
| PA |
| ||
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |