题目内容
已知△ABC中,D是AB的中点,E是BC的三等分点(BE>CE),AE,CD交于点F.求证:F是CD的中点.
考点:三角形中位线定理
专题:证明题
分析:作DM∥AE交BC于点M,则DM是△ABE的中位线,即M是BE的中点,然后证明EF是△CDM的中位线即可.
解答: 证明:作DM∥AE交BC于点M.
证明:作DM∥AE交BC于点M.
又∵D是AB的中点,
∴DM是BE的中位线,
∴M是BM的中点,
又∵E是BC的三等分点,
∴E是MC的中点,
又∵DM∥AE,
∴EF是△CDM的中位线,F是CD的中点.
 证明:作DM∥AE交BC于点M.
证明:作DM∥AE交BC于点M.又∵D是AB的中点,
∴DM是BE的中位线,
∴M是BM的中点,
又∵E是BC的三等分点,
∴E是MC的中点,
又∵DM∥AE,
∴EF是△CDM的中位线,F是CD的中点.
点评:本题考查了平行线分线段成比例定理,正确作出辅助线,得到DM是△ABE的中位线是关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
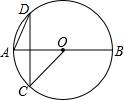 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )| A、70° | B、130° |
| C、140° | D、160° |
若
在实数范围内有意义,则x的取值范围是( )
| x-3 |
| A、x>0 | B、x>3 |
| C、x≤3 | D、x≥3 |
 如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF=
如图,△ABC中,∠CAB=120°,AB,AC的垂直平分线分别交BC于点E、F,则∠EAF= 如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.
如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF. 如图,已知△ABC≌△AFE,若∠ACB=65°,则∠EAC等于
如图,已知△ABC≌△AFE,若∠ACB=65°,则∠EAC等于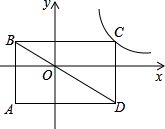 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=