题目内容
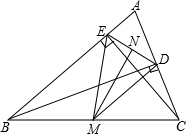 如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M、N分别是BC、DE的中点,连接ME、MD.
如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,点M、N分别是BC、DE的中点,连接ME、MD.(1)求证:MN⊥DE;
(2)若∠A=60°,试判定△MED的形状.
考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得MD=ME=
BC,再根据等腰三角形三线合一的性质证明即可;
(2)根据等腰三角形两底角相等求出∠BME+∠CMD,然后求出∠DME=60°,再根据等边三角形的判定方法解答.
| 1 |
| 2 |
(2)根据等腰三角形两底角相等求出∠BME+∠CMD,然后求出∠DME=60°,再根据等边三角形的判定方法解答.
解答:(1)证明:∵BD⊥AC于D,CE⊥AB于E,点M是BC的中点,
∴MD=ME=
BC,
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°-2∠ABC+180°-2∠ACB=360°-2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∴∠BME+∠CMD=360°-2×120°=120°,
∴∠DME=60°,
∴△MED是等边三角形.
∴MD=ME=
| 1 |
| 2 |
∴点N是DE的中点,
∴MN⊥DE;
(2)解:∵MD=ME=BM=CM,
∴∠BME+∠CMD=180°-2∠ABC+180°-2∠ACB=360°-2(∠ABC+∠ACB),
∵∠A=60°,
∴∠ABC+∠ACB=180°-60°=120°,
∴∠BME+∠CMD=360°-2×120°=120°,
∴∠DME=60°,
∴△MED是等边三角形.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,等边三角形的判定,熟记性质是解题的关键,难点在于(2)求出∠DME=60°.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有( )
如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有( )| A、1种 | B、2种 | C、3种 | D、4种 |
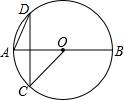 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=70°,则∠BOC=( )| A、70° | B、130° |
| C、140° | D、160° |
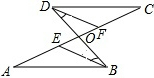 如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
如图,已知:∠A=∠C,∠CDF=∠ABE,求证:∠FDB=∠EBD.
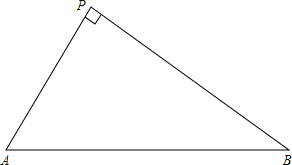 有一块直角三角形的菜地,如图所示,∠P=90°,PA=20m,PB=
有一块直角三角形的菜地,如图所示,∠P=90°,PA=20m,PB= 如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.
如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.