题目内容
1.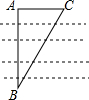 如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )| A. | asinα | B. | acosα | C. | atanα | D. | $\frac{a}{tanα}$ |
分析 根据题意,可得Rt△ABC,同时可知AC与∠ACB.根据三角函数的定义解答.
解答 解:根据题意,在Rt△ABC,有AC=a,∠ACB=α,且tanα=$\frac{AB}{AC}$,
则AB=AC×tanα=a•tanα,
故选C.
点评 本题考查了解直角三角形的应用,要熟练掌握三角函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{48}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{4a+4}$ | D. | $\sqrt{14}$ |
9.济南市名校德润中学九年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了$\frac{1}{3}$小时后,其余学生乘汽车出发,结果他们同时达到,已知乘汽车学生的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为每小时x千米,则所列方程正确的是( )
| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
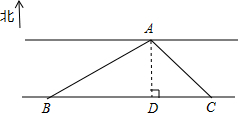 聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)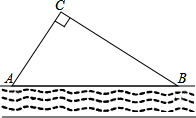 某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)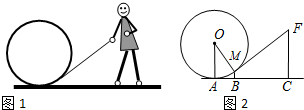
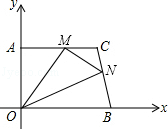 在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4).
在平面直角坐标系中,直角梯形AOBC的位置图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别在线段AC、线段BC上运动,当△MON的面积达到最大时,存在一种使得△MON周长最小的情况,则此时点M的坐标为(3,4).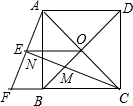 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.