题目内容
11.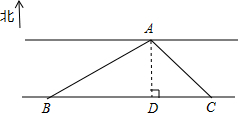 聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
聪明的小亮运用数学知识帮爸爸测量河的宽度,测量过程如图所示,在河岸B点测得对岸一水站在北偏东60°的方向上,沿河岸行走300m到达C处,此时测得点A在北偏西45°方向上,你能根据这些数据帮小亮计算出河的宽度AD的值吗?写明你计算的过程.($\sqrt{2}≈1.4$,$\sqrt{3}≈1.7$,结果保留一位小数)
分析 作AD⊥BC于D,设河宽AD为x,根据BD+CD=300,列出方程即可解决问题.
解答 解:作AD⊥BC于D, 设河宽AD为x
设河宽AD为x
由题意可得∠ABC=30°,∠BCA=45°
在直角三角形ABD中,∵∠ADB=90°,∠ABD=30°AD=x,
∴BD=$\sqrt{3}$x,
在直角三角形ACD中,AD=CD=x
∵BC=BD+CD
∴$\sqrt{3}$x+x=300
解得x=150($\sqrt{3}$-1)≈105.
故测得河宽约为105米.
点评 本题考查方向角、解直角三角形等知识,解题的关键是添加辅助线构造直角三角形,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
1.计算(-2)-(-6)的结果等于( )
| A. | 4 | B. | -4 | C. | 8 | D. | -8 |
20.下列标志既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.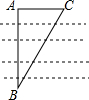 如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
 如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )| A. | asinα | B. | acosα | C. | atanα | D. | $\frac{a}{tanα}$ |
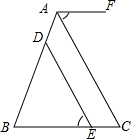 如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2
如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2