题目内容
13.图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=$\frac{3}{5}$.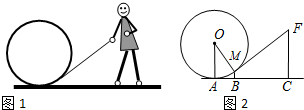
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55cm,求铁环钩MF的长度.
分析 (1)过M作与AC平行的直线,与OA、FC分别相交于H、N.那么求BM的长就转化为求HA的长,而要求出HA,必须先求出OH,在直角三角形OHM中,sinα的值,且铁环的半径为5个单位即OM=5,可求得HM的值,从而求得HA的值;
(2)因为∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH,又因为sin∠MOA=$\frac{3}{5}$,所以可得出FN和FM之间的数量关系,即FN=$\frac{3}{5}$FM,再根据MN=11-3=8,利用勾股定理即可求出FM=10个单位.
解答 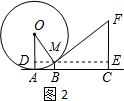 解:(1)过点M作MD⊥OA交OA于点D,
解:(1)过点M作MD⊥OA交OA于点D,
在RT△ODM中,sinα=$\frac{DM}{OM}=\frac{3}{5}$,
∴DM=15cm∴OD=20 cm,
∴AD=BM=5cm;
(2)延长DM交CF于点E,
易得:∠FME=∠AOM=α,
∵ME=AC-DM=55-15=40cm,
∴cosα=$\frac{ME}{MF}=\frac{4}{5}$
∴MF=50cm.
点评 考查了解直角三角形的应用,解此题的关键是把实际问题转化为数学问题,只要把实际问题抽象到解直角三角形中即可解答.

练习册系列答案
相关题目
4.把-2+(+3)-(-5)+(-4)-(+3)写成省略括号和的形式,正确的是( )
| A. | -2+3-5-4-3 | B. | -2+3+5-4+3 | C. | -2+3+5+4-3 | D. | -2+3+5-4-3 |
1.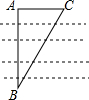 如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
 如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )
如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=α,则A、B两点的距离为( )| A. | asinα | B. | acosα | C. | atanα | D. | $\frac{a}{tanα}$ |
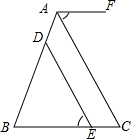 如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2
如图,点D、E分别在AB、BC上,AF∥BC,DE∥AC.求证:∠1=∠2