题目内容
2. 如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.
如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.
分析 由角的互余关系和已知条件得出∠A=∠1,由ASA证明△ABC≌△ECD,得出对应边相等即可.
解答 证明:∵AB⊥BC,DC⊥AC,
∴∠B=∠DCE=90°,
∴∠A+∠ACB=90°,∠ACB+∠2=90°,
∴∠A=∠2,
∵∠1=∠2,
∴∠A=∠1,
在△ABC和△ECD中,$\left\{\begin{array}{l}{∠A=∠1}&{\;}\\{AB=EC}&{\;}\\{∠B=∠DCE}&{\;}\end{array}\right.$,
∴△ABC≌△ECD(ASA),
∴AC=ED.
点评 本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定与性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
17.已知m,n均不等于0,且m-n=2mn,则$\frac{2}{m}-\frac{2}{n}$的值是( )
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
19.把12+(+9)+(-6)写成省略加号的和的形式,正确的是( )
| A. | 12-9-6 | B. | 12+9-6 | C. | -12+9+6 | D. | 12-9+6 |
 如图,Rt△ABC中,∠C=90°,D是AB的中点,若AB=10,则CD的长等于5.
如图,Rt△ABC中,∠C=90°,D是AB的中点,若AB=10,则CD的长等于5.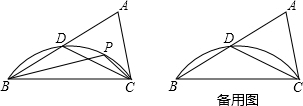
 如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
如图,已知抛物线y=-$\frac{1}{4}{x^2}$+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).