题目内容
13.写出二次函数y=x2-8x-8的图象顶点坐标和对称轴的位置并求出它的最值.分析 运用配方法把函数的一般式化为顶点式,写出顶点坐标、对称轴和最小值即可.
解答 解:y=x2-8x-8=(x-4)2-24,顶点坐标为(4,-24),对称轴为直线x=4,
∵a=1>0,
∴函数有最小值-24.
点评 本题考查的是二次函数的图象和性质,用配方法把函数的一般式化为顶点式是解题的关键,解答时,要熟练运用函数的性质.

练习册系列答案
相关题目
8.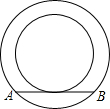 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
 如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
如图,两个同心圆的直径分别为6cm和10cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
10.抛物线y=ax2+bx+c(a>0)的对称轴为x=1,它与x轴的一个交点的坐标为(-3,0),则它与x轴另一个交点的坐标为( )
| A. | (-2,0) | B. | (-1,0) | C. | (2,0) | D. | (5,0) |
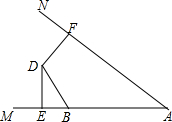 如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.
如图,D是∠MAN内部一点,点B是射线AM上一点,DE⊥AM于E,DF⊥AN于F,且DE=DF,在射线AN上取一点C,使得DC=DB,问∠ABD与∠ACD有什么数量关系?请说明理由.



 小王在一路灯下A、C两点的影长AB、CD如图所示.
小王在一路灯下A、C两点的影长AB、CD如图所示. 画出下列各三角形BC边上的高AD.
画出下列各三角形BC边上的高AD. 如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.
如图,AB⊥BC,DC⊥AC,垂足分别为B、C,∠1=∠2,AB=EC.求证:AC=ED.