题目内容
17.某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.(Ⅰ)某月该单位用水2800吨,水费是1400元;若用水3200吨,水费是1660元;
(Ⅱ)设该单位每月用水量为x吨,水费为y元,求y关于x的函数解析式;
(Ⅲ)若某月该单位缴纳水费1540元,求该单位这个月用水多少吨?
分析 (1)根据3000吨以内,用水每吨收费0.5元,超计划部分每吨按0.8元收费,即可求解;
(2)根据收费标准,分0≤x≤3000吨和x>3000吨两种情况进行讨论,分两种情况写出解析式;
(3)该单位缴纳水费1540元一定是超过3000元,根据超过3000吨的情况的水费标准即可得到一个关于用水量的方程,即可求解.
解答 解:(1)若用水2800吨,水费是:2800×0.5=1400元;
该单位用水3200吨,水费是:3000×0.5+200×0.8=1660元;
故答案为:1400,1660;
(2)根据题意可得:当0≤x≤3000时,y=0.5x,
当x>3000时,
y=0.5×3000+0.8(x-3000)
=1500+0.8x-2400
=0.8x-900,
故y关于x的函数关系式为:y=$\left\{\begin{array}{l}{0.5x(0≤x≤3000)}\\{0.8x-900(x>3000)}\end{array}\right.$;
(3)因为缴纳水费1540元,所以用水量应超过3000吨,故令,设用水x吨.
1500+0.8(x-3000)=1540
解得:x=3050
即该月的用水量是3050吨.
点评 本题考查的是用一次函数解决实际问题,正确理解收费标准,列出函数解析式是关键,此类题是近年中考中的热点问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2. 某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
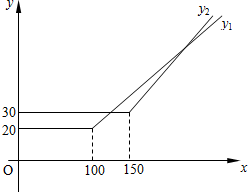
设每月通话时间为x分种,A,B两种套餐每月话费分别为y1,y2元.y1,y2关于x的函数图象如图所示.
(1)表格中的a=20,b=150;
(2)通话时间超过每月免费通话时间后,求y1,y2关于x的函数关系式,并写出相应的取值范围;
(3)已知甲乙两人分别使用A,B两种套餐,他们的通话时间都是t分钟(t>150),但话费相差5元,求两人的通话时间.
 某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
某电信公司提供的移动通讯服务的收费标准有两种套餐如表:| A套餐 | B套餐 | |
| 每月基本服务费 | a | 30 |
| 每月免费通话时间 | 100 | b |
| 超出每分钟收费 | 0.4 | 0.5 |
(1)表格中的a=20,b=150;
(2)通话时间超过每月免费通话时间后,求y1,y2关于x的函数关系式,并写出相应的取值范围;
(3)已知甲乙两人分别使用A,B两种套餐,他们的通话时间都是t分钟(t>150),但话费相差5元,求两人的通话时间.
 如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
如图所示,某教学活动小组选定测量山顶铁塔AE的高,他们在30m高的楼CD的底部点D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角为36°52′.若小山高BE=62m,楼的底部D与山脚在同一水平面上,求铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)