题目内容
7．先化简，再求值：（$\frac{1}{a-1}-\frac{2}{{a}^{2}-a}$）$÷（a+1-\frac{4a-5}{a-1}）$，其中a是方程x2+2x-3=0的解．分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出已知方程的解得到a的值，代入计算即可求出值．
解答 解：原式=$\frac{a-2}{a（a-1）}$÷$\frac{{a}^{2}-1-4a+5}{a-1}$=$\frac{a-2}{a（a-1）}$•$\frac{a-1}{（a-2）^{2}}$=$\frac{1}{{a}^{2}-2a}$，
把x=a代入方程得：a2+2a-3=0，即（a-1）（a+3）=0，
解得：a=1（舍去）或a=-3，
则当a=-3时，原式=$\frac{1}{15}$．
点评 此题考查了分式的化简运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
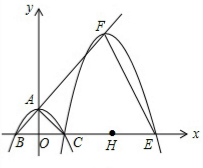如图，抛物线y=ax2+c（a≠0）与y轴交于点A，与x轴交于点B，C两点（点C在x轴正半轴上），△ABC为等腰直角三角形，且面积为4．现将抛物线沿BA方向平移，平移后的抛物线经过点C时，与x轴的另一交点为E，其顶点为F，对称轴与x轴的交点为H．
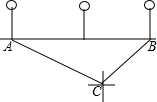周末，小明一家去东昌湖划船，当船划到湖中C点处时，湖边的路灯A位于点C的北偏西64°方向上，路灯B位于点C的北偏东44°方向上，已知每两个路灯之间的距离是50米，求此时小明一家离岸边的距离是多少米？（精确到1米）（参考数据：
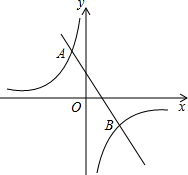如图，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A（-2，6）和点B（4，n）．
17．下列计算正确的是（ ）
| A． | $\sqrt{a}$+$\sqrt{b}$=$\sqrt{ab}$ | B． | （-a2）2=-a4 | C． | （a-2）2=a2-4 | D． | $\sqrt{a}$÷$\sqrt{b}$=$\sqrt{\frac{a}{b}}$（a≥0，b＞0） |