题目内容
13.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m<0}\\{x+m>2}\end{array}\right.$无解,则m的取值范围为( )| A. | m>-$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m<-$\frac{2}{3}$ | D. | m≥-$\frac{2}{3}$ |
分析 先解不等式的解集,然后根据不等式组无解得出m的取值范围即可.
解答 解:$\left\{\begin{array}{l}{x-2m<0①}\\{x+m>2②}\end{array}\right.$
解不等式①得:x<2m,
解不等式②得:x>2-m,
∵关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m<0}\\{x+m>2}\end{array}\right.$无解,
∴2m≤2-m,
解得:m≤$\frac{2}{3}$.
故选B.
点评 本题考查了解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
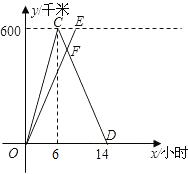 已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即沿原路返回,如图是它们离A城的距离y(千米)与行驶时间x(小时)之间的函数图象.