题目内容
2.在直角坐标系中,点A、B的坐标分别为(-2,4)、(-5,2),点M在x轴上,点N在y轴上.如果以点A、B、M、N为顶点的四边形是平行四边形,那么符合条件的点M有3个.分析 利用一组对边相等且平行的四边形是平行四边形进而得出答案.
解答 解:如图所示:当AB平行且等于NM时,四边形ABMN是平行四边形,
当AB平行且等于N′M′时,四边形ABN′M′是平行四边形.
当AB为对角线时,四边形ABN′M′是平行四边形.
故符合题意的有3个点.
故答案为:3.
点评 此题考查了平行四边形的判定,结合AB的长分别确定M,N的位置是解决问题的关键.

练习册系列答案
相关题目
13.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m<0}\\{x+m>2}\end{array}\right.$无解,则m的取值范围为( )
| A. | m>-$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m<-$\frac{2}{3}$ | D. | m≥-$\frac{2}{3}$ |
10. 如图,已知a∥b,直线c与a,b相交,∠1=60°,∠2=70°,则∠3等于( )
如图,已知a∥b,直线c与a,b相交,∠1=60°,∠2=70°,则∠3等于( )
 如图,已知a∥b,直线c与a,b相交,∠1=60°,∠2=70°,则∠3等于( )
如图,已知a∥b,直线c与a,b相交,∠1=60°,∠2=70°,则∠3等于( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
17.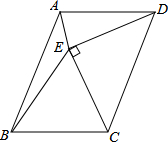 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 45° |
14.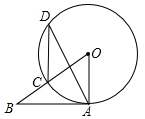 如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
 如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )| A. | 29° | B. | 30° | C. | 31° | D. | 32° |
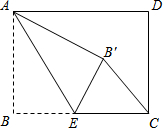 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.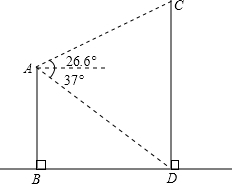 如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.
如图,平地上一幢建筑物AB与铁塔CD相距40m,在建筑物的顶部测得铁塔底部的俯角为37°,测得铁塔顶部的仰角为26.6°,求铁塔的高度.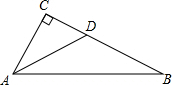 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,CD=5cm,则BD的长是10cm.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,CD=5cm,则BD的长是10cm.