题目内容
4.两游艇自某地同时出发,一艇以10千米/小时的速度向正北航行,另一艇以7千米/小时的速度向北偏东45度方向行驶,问:经过40分钟,两艇相距多远?分析 首先画出示意图,由题意可得,OA=10×$\frac{40}{60}$=$\frac{20}{3}$千米,OB=7×$\frac{40}{60}$=$\frac{14}{3}$千米,∠AOB=45°.作AC⊥OB于C.由∠AOC=45°,∠ACO=90°,得出△AOC是等腰直角三角形,那么AC=OC=$\frac{\sqrt{2}}{2}$OA=$\frac{10\sqrt{2}}{3}$千米,于是BC=OC-OB=$\frac{10\sqrt{2}-14}{3}$千米,再根据勾股定理即可求出AB.
解答 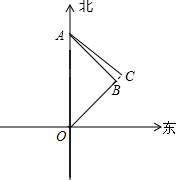 解:如图,经过40分钟,两游艇分别到达A、B两点.
解:如图,经过40分钟,两游艇分别到达A、B两点.
由题意可得,OA=10×$\frac{40}{60}$=$\frac{20}{3}$千米,OB=7×$\frac{40}{60}$=$\frac{14}{3}$千米,∠AOB=45°.
作AC⊥OB于C.
∵∠AOC=45°,∠ACO=90°,
∴△AOC是等腰直角三角形,
∴AC=OC=$\frac{\sqrt{2}}{2}$OA=$\frac{\sqrt{2}}{2}$×$\frac{20}{3}$=$\frac{10\sqrt{2}}{3}$千米,
∴BC=OC-OB=$\frac{10\sqrt{2}}{3}$-$\frac{14}{3}$=$\frac{10\sqrt{2}-14}{3}$千米,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{(\frac{10\sqrt{2}}{3})^{2}+(\frac{10\sqrt{2}-14}{3})^{2}}$=$\frac{\sqrt{596-280\sqrt{2}}}{3}$千米.
答:经过40分钟,两艇相距$\frac{\sqrt{596-280\sqrt{2}}}{3}$千米.
点评 本题考查了解直角三角形的应用-方向角问题,等腰直角三角形的判定与性质,勾股定理,根据方向角的定义准确画出图形作出辅助线构造直角三角形是解题的关键.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案| A. | 855.6×108 | B. | 8.556×108 | C. | 8.556×1011 | D. | 8.556×1010 |
| A. | 19.4×108 | B. | 1.94×108 | C. | 1.94×109 | D. | 19.4×109 |
| A. | m>-$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m<-$\frac{2}{3}$ | D. | m≥-$\frac{2}{3}$ |
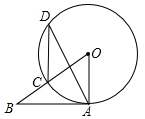 如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )
如图,AB为⊙O的切线,切点为A,BO交⊙O于点C,点D在⊙O上,若∠ABO的度数是32°,则∠ADC的度数是( )| A. | 29° | B. | 30° | C. | 31° | D. | 32° |
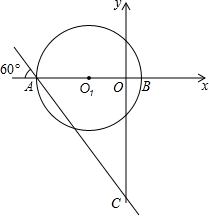 在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.
在平面直角坐标系中,点O1的坐标为(-4,0),以点O1为圆心8为半径的圆与x轴交于A,B两点.过点A作直线L与x轴负方向成60°的角,且交y轴于点C.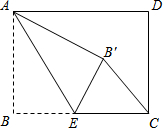 如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.
如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,求BE的长.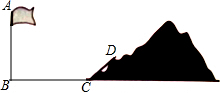 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).