题目内容
8.计算:①($\frac{2}{3}$)-1+(π-3)0+(-$\frac{1}{2}$)-2-25;
②2a3•a3-(-3a2)2•a2+a7÷(-a);
③(2x-y)2(2x+y)2;
④4(x+2)2-(2x+3)(3x-2).
分析 ①首先利用零指数幂的性质以及负指数幂的性质分别化简各数进而求出即可;
②直接利用同底数幂的乘除法运算法则化简,进而求出即可;
③直接利用完全平方公式以及平方差公式化简求出即可;
④直接利用多项式乘法以及乘法公式计算得出即可.
解答 解:①($\frac{2}{3}$)-1+(π-3)0+(-$\frac{1}{2}$)-2-25
=$\frac{3}{2}$+1+4-32
=-25.5;
②2a3•a3-(-3a2)2•a2+a7÷(-a)
=2a6-9a6-a6
=-8a6;
③(2x-y)2(2x+y)2
=(4x2-y2)2
=16x4-8x2y2+y4;
④4(x+2)2-(2x+3)(3x-2)
=4(x2+4x+4)-(6x2-4x+9x-6)
=4x2+16x+16-6x2-5x+6
=-2x2+11x+22.
点评 此题主要考查了整式的混合运算以及实数运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
19.丹东市2014年前三季度全市实现地区生产总值855.6亿元,用科学记数法表示为( )
| A. | 855.6×108 | B. | 8.556×108 | C. | 8.556×1011 | D. | 8.556×1010 |
13.若关于x的一元一次不等式组$\left\{\begin{array}{l}{x-2m<0}\\{x+m>2}\end{array}\right.$无解,则m的取值范围为( )
| A. | m>-$\frac{2}{3}$ | B. | m≤$\frac{2}{3}$ | C. | m<-$\frac{2}{3}$ | D. | m≥-$\frac{2}{3}$ |
17.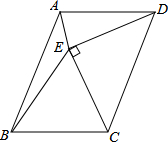 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
 如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )
如图,以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE,使AD=DE=CE,∠DEC=90°,且点E在平行四边形内部,连接AE、BE,则∠AEB的度数是( )| A. | 120° | B. | 135° | C. | 150° | D. | 45° |
18.要使式子$\sqrt{2+x}$有意义,则x的取值范围是( )
| A. | x≤-2 | B. | x≤2 | C. | x≥2 | D. | x≥-2 |
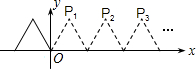 如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方向连续翻折2015次,依次得到点P1,P2,P3,…P2015,则点P2015的坐标是(4029,$\sqrt{3}$).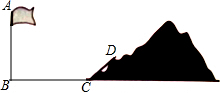 如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米).
如图,学校旗杆附近有一斜坡,小明准备测量旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影子长BC=20米,斜坡坡面上的影子CD=8米,太阳光AD与水平地面BC成30°角,斜坡CD与水平地面BC成45°的角,求旗杆AB的高度.($\sqrt{3}$=1.732,$\sqrt{2}$=1.414,$\sqrt{6}$=2.449,精确到1米). 图“E”中同旁内角有3对.
图“E”中同旁内角有3对.