题目内容
2.三张完全相同的卡片上分别写有函数y=-2x-3,y=$\frac{3}{x}$,y=x2+1,从中随机抽取一张,则所得函数的图象在第一象限内y随x的增大而增大的概率是$\frac{1}{3}$.分析 先求出函数的图象在第一象限内y随x的增大而增大的函数的个数,再根据概率公式即可得出答案.
解答 解:∵函数y=-2x-3,y=$\frac{3}{x}$,y=x2+1中,在第一象限内y随x的增大而增大的只有y=x2+1一个函数,
∴所得函数的图象在第一象限内y随x的增大而增大的概率是$\frac{1}{3}$;
故答案为:$\frac{1}{3}$.
点评 此题考查了概率公式,掌握一次函数、反比例函数和二次函数的性质是本题的关键,用到的知识点是概率=所求情况数与总情况数之比.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
10.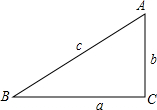 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.下列各组数,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 8,15,17 | C. | 5,10,13 | D. | 8,39,40 |
 是方程
是方程 的一个根,那么
的一个根,那么 的值是_____.
的值是_____. 如图,AD是△ABC的BC边上的中线,若△ABC的面积是6,则△ACD的面积是3.
如图,AD是△ABC的BC边上的中线,若△ABC的面积是6,则△ACD的面积是3. 如图,平面上有四个点A,B,C,D,根据下列语句画图.
如图,平面上有四个点A,B,C,D,根据下列语句画图. 如图,∠D=∠C=90°,AC=BD.求证:AD=BC.
如图,∠D=∠C=90°,AC=BD.求证:AD=BC.