题目内容
11.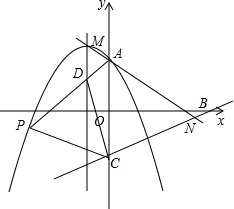 已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.(1)若直线BC和抛物线有两个不同交点,求a的取值范围,并用a表示交点M,A的坐标;
(2)将△NAC沿着y轴翻转,若点N的对称点P恰好落在抛物线上,AP与抛物线的对称轴相交于点D,连接CD,求a的值及△PCD的面积;
(3)在抛物线y=-x2-2x+a(a>0)上是否存在点P,使得以P,A,C,N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)先联立抛物线与直线的解析式得出关于x的方程,再由直线BC和抛物线有两个不同交点可知△>0,求出a的取值范围,令x=0求出y的值即可得出A点坐标,把抛物线的解析式化为顶点式的形式即可得出M点的坐标;
(2)利用待定系数法求出直线MA的解析式,联立两直线的解析式可得出N点坐标,进而可得出P点坐标,根据S△PCD=S△PAC-S△ADC可得出结论;
(3)分点P在y轴左侧与右侧两种情况进行讨论即可.
解答 解:(1)由题意得,$\left\{\begin{array}{l}y=-{x}^{2}-2x+a\\ y=\frac{1}{2}x-a\end{array}\right.$,整理得2x2+5x-4a=0.
∵△=25+32a>0,解得a>-$\frac{25}{32}$.
∵a≠0,
∴a>-$\frac{25}{32}$且a≠0.
令x=0,得y=a,
∴A(0,a).
由y=-(x+1)2+1+a得,M(-1,1+a).
(2)设直线MA的解析式为y=kx+b(k≠0),
∵A(0,a),M(-1,1+a),
∴$\left\{\begin{array}{l}1+a=-k+b\\ a=b\end{array}\right.$,解得$\left\{\begin{array}{l}k=-1\\ b=a\end{array}\right.$,
∴直线MA的解析式为y=-x+a,
联立得,$\left\{\begin{array}{l}y=-x+a\\ y=\frac{1}{2}x-a\end{array}\right.$,解得$\left\{\begin{array}{l}x=\frac{4a}{3}\\ y=-\frac{a}{3}\end{array}\right.$,
∴N($\frac{4a}{3}$,-$\frac{a}{3}$).
∵点P是点N关于y轴的对称点,
∴P(-$\frac{4a}{3}$,-$\frac{a}{3}$).
代入y=-x2-2x+a得,-$\frac{a}{3}$=-$\frac{16}{9}$a2+$\frac{8}{3}$a+a,解得a=$\frac{9}{4}$或a=0(舍去).
∴A(0,$\frac{9}{4}$),C(0,-$\frac{9}{4}$),M(-1,$\frac{13}{4}$),|AC|=$\frac{9}{2}$,
∴S△PCD=S△PAC-S△ADC=$\frac{1}{2}$|AC|•|xp|-$\frac{1}{2}$|AC|•|x0|
=$\frac{1}{2}$•$\frac{9}{2}$•(3-1)
=$\frac{9}{2}$;
(3)①当点P在y轴左侧时,
∵四边形APCN是平行四边形,
∴AC与PN互相平分,N($\frac{4a}{3}$,-$\frac{a}{3}$),
∴P(-$\frac{4a}{3}$,$\frac{a}{3}$);
代入y=-x2-2x+a得,$\frac{a}{3}$=-$\frac{16}{9}$a2+$\frac{8}{3}$a+a,解得a=$\frac{15}{8}$,
∴P1(-$\frac{5}{2}$,$\frac{5}{8}$).
②当点P在y轴右侧时,
∵四边形ACPN是平行四边形,
∴NP∥AC且NP=AC,
∵N($\frac{4a}{3}$,-$\frac{a}{3}$),A(0,a),C(0,-a),
∴P($\frac{4a}{3}$,-$\frac{7a}{3}$).
代入y=-x2-2x+a得,-$\frac{7a}{3}$=-$\frac{16}{9}$a2-$\frac{8}{3}$a+a,解得a=$\frac{3}{8}$,
∴P2($\frac{1}{2}$,-$\frac{7}{8}$).
综上所述,当点P1(-$\frac{5}{2}$,$\frac{5}{8}$)和P2($\frac{1}{2}$,-$\frac{7}{8}$)时,A、C、P、N能构成平行四边形.
点评 本题考查的是二次函数综合题,涉及到二次函数与一次函数的交点问题、二次函数图象上点的坐标特点、平行四边形的判定与性质等知识,难度较大.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图是正方体的一个平面展开图,原正方体上两个“我”字所在面的位置关系是( )
如图是正方体的一个平面展开图,原正方体上两个“我”字所在面的位置关系是( )| A. | 相对 | B. | 相邻 | C. | 相隔 | D. | 重合 |

 如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是4.
如图,△ABC三边的中线AD、BE、CF的公共点为G,若S△ABC=12,则图中阴影部分的面积是4.
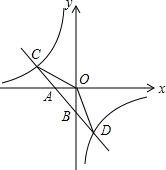 如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.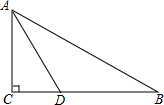 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=2.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1,则BD=2.