题目内容
1.在⊙O中,弦AB和弦AC构成的∠BAC=48°,M、N分别是AB和AC的中点,则∠MON的度数为132°或48°.分析 连接OM,ON,利用垂径定理得OM⊥AB,ON⊥AC,再分类讨论,当AB,AC在圆心异侧时(如图1),利用四边形内角和得结果;
当AB,AC在圆心同侧时(如图2),利用相似三角形的性质得结果.
解答 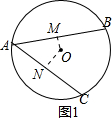 解:连接OM,ON,
解:连接OM,ON,
∵M、N分别是AB和AC的中点,
∴OM⊥AB,ON⊥AC,
OM⊥AB,ON⊥AC,
当AB,AC在圆心异侧时(如图1),
∵∠BAC=48°,
在四边形AMON中,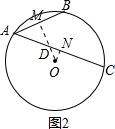
∴∠MON=360°-90°-90°-48°=132°;
当AB,AC在圆心同侧时(如图2),
∵∠ADM=∠ODN,∠AMD=∠OND,
∴△ADM∽△ODN,
∴∠MON=∠BAC=48°.
故答案为:132°或48°.
点评 本题主要考查了垂径定理,分类讨论,数形结合是解答此题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
9.下列运算正确的是( )
| A. | x2+x4=x6 | B. | x6÷x3=x2 | ||
| C. | $\frac{-a-b}{a+b}$=-1 | D. | $\frac{b}{{a}^{2}-{b}^{2}}$÷(1-$\frac{a}{a+b}$)=-$\frac{1}{a-b}$ |
13.某工厂现在平均每天比原计划多生产30台机器,现在生产500台机器所需时间与圆计划生产350台机器所需时间相同.设原计划平均每天生产x台机器,下面所列方程正确的是( )
| A. | $\frac{500}{x+30}=\frac{350}{x}$ | B. | $\frac{500}{x-30}=\frac{350}{x}$ | C. | $\frac{500}{x}=\frac{350}{x-30}$ | D. | $\frac{500}{x}=\frac{350}{x+30}$ |
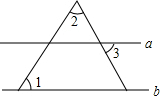 如图,a∥b,∠1=55°,∠2=65°,则∠3的大小为60°.
如图,a∥b,∠1=55°,∠2=65°,则∠3的大小为60°. 如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )
如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )



 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.
为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.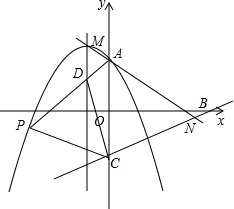 已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.