题目内容
16.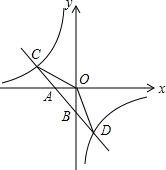 如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.
如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.(1)求一次函数y1=k1x+b与反比例函数y2=$\frac{{k}_{2}}{x}$的解析式;
(2)求△COD的面积;
(3)直接写出y1>y2时自变量x的取值范围.
分析 (1)把点D的坐标代入y2=$\frac{{k}_{2}}{x}$利用待定系数法即可求得反比例函数的解析式,作DE⊥x轴于E,根据题意求得A的坐标,然后利用待定系数法求得一次函数的解析式;
(2)联立方程求得C的坐标,然后根据S△COD=S△AOC+S△AOD即可求得△COD的面积;
(3)根据图象即可求得.
解答 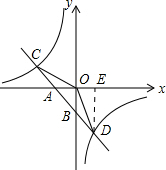 解:∵点D(2,-3)在反比例函数y2=$\frac{{k}_{2}}{x}$的图象上,
解:∵点D(2,-3)在反比例函数y2=$\frac{{k}_{2}}{x}$的图象上,
∴k2=2×(-3)=-6,
∴y2=-$\frac{6}{x}$;
作DE⊥x轴于E,
∵D(2,-3),点B是线段AD的中点,
∴A(-2,0),
∵A(-2,0),D(2,-3)在y1=k1x+b的图象上,
∴$\left\{\begin{array}{l}{-2{k}_{1}+b=0}\\{2{k}_{1}+b=-3}\end{array}\right.$,
解得k1=-$\frac{3}{4}$,b=-$\frac{3}{2}$,
∴y1=-$\frac{3}{4}$x-$\frac{3}{2}$;
(2)由$\left\{\begin{array}{l}{y=-\frac{3}{4}x-\frac{3}{2}}\\{y=-\frac{6}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-4}\\{{y}_{2}=\frac{3}{2}}\end{array}\right.$,
∴C(-4,$\frac{3}{2}$),
∴S△COD=S△AOC+S△AOD=$\frac{1}{2}$×$2×\frac{3}{2}$+$\frac{1}{2}$×2×3=$\frac{9}{2}$;
(3)当x<-4或0<x<2时,y1>y2.
点评 本题考查了反比例函数和一次函数的交点问题,待定系数法求一次函数和二次函数的解析式,方程组的解以及三角形的面积等,求得A点的坐标是解题的关键.

 ,
,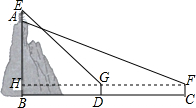 学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下: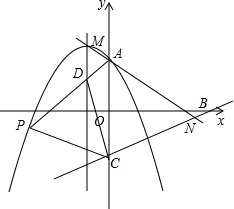 已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.
已知抛物线y=-x2-2x+a(a≠0)与y轴相交于A点,顶点为M,直线y=$\frac{1}{2}$x-a分别与x轴、y轴相交于B,C两点,并且与直线MA相交于N点.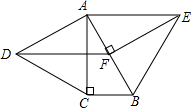 如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.
如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$时,四边形ADFE是平行四边形.