题目内容
2.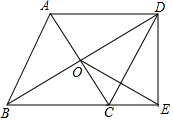 如图,菱形ABCD的对角线相交于点O,DE⊥BC的延长线于点E,若菱形的周长为20,AC=6,则线段OE的长是4.
如图,菱形ABCD的对角线相交于点O,DE⊥BC的延长线于点E,若菱形的周长为20,AC=6,则线段OE的长是4.
分析 先根据菱形的四边相等得:边长AD=5,由勾股定理求OD=4,则BD=8,再根据直角三角形斜边中线等于斜边一半求OE的长.
解答 解:∵四边形ABCD是菱形,
∴AC⊥BD,AO=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,OB=OD,
∵菱形的周长为20,
∴AD=5,
在Rt△AOD中,由勾股定理得:OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴BD=2OD=8,
∵DE⊥BC,
∴∠DEB=90°,
∵OD=OB,
∴OE=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
故答案为:4.
点评 本题考查了菱形的性质、直角三角形斜边中线的性质、勾股定理,熟练掌握菱形的性质是关键:①菱形的四边相等,根据周长可求边长;②菱形的对角线互相垂直且平分.

练习册系列答案
相关题目
12.下列调查中,最合适采用普查方式的是( )
| A. | 调查一批汽车的使用寿命 | |
| B. | 调查山东省市民春节期间计划外出旅游情况 | |
| C. | 调查某航班的旅客是否携带了违禁物品 | |
| D. | 调查全国初三学生的视力情况 |
17.对于函数y=-2x+4.下列说法错误的是( )
| A. | y随x的增大而减小 | B. | 它的图象与y轴的交点是(0,4) | ||
| C. | 当x<2时,y<0 | D. | 它的图象不经过第三象限 |
7.某商场服装部为了调动营业员的积极性,决定实行目标管理.为了确定一个适当的月销售日标,服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
(1)分别求出所有营业员月销售额的众数、中位数和平均数;
(2)如果想让一半左右的营业员有信心达到销售目标.月销售目标定为多少合适?
| 销售额/万元 | 14 | 15 | 17 | 19 | 27 | 30 |
| 人数 | 1 | 6 | 3 | 4 | 5 | 1 |
(2)如果想让一半左右的营业员有信心达到销售目标.月销售目标定为多少合适?
11.下列命题是真命题的是( )
| A. | 若a>b,则ac>bc | B. | 若ac>bc,则a>b | C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
12.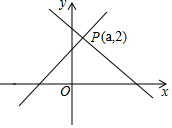 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
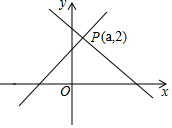 如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )
如图,直线y=x+1与直线y=mx+n相交于点P(a,2),则关于不等式x+1≥mx+n的解集是( )| A. | x≥-1 | B. | 0≤x≤1 | C. | x≥1 | D. | x≤1 |
 如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.
如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.