题目内容
10. 如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.
如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.
分析 先根据三角形内角和定理求出∠DBC+∠DCB的度数,进而可得出∠BDC的度数.
解答 解:∵∠ABD=40°,∠ACD=35°,∠A=55°,
∴∠DBC+∠DCB=180°-40°-35°-55°=50°,
∴∠BDC=180°-50°=130°.
故答案为:130°
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
20.式子$\sqrt{x+2}$在实数范围内有意义,则x的取值范围是( )
| A. | x>-2 | B. | x≤-2 | C. | x<-2 | D. | x≥-2 |
1. 如图,AD和BC相交于O点,OA=OC,用“SAS”证明△AOB≌△COD还需( )
如图,AD和BC相交于O点,OA=OC,用“SAS”证明△AOB≌△COD还需( )
 如图,AD和BC相交于O点,OA=OC,用“SAS”证明△AOB≌△COD还需( )
如图,AD和BC相交于O点,OA=OC,用“SAS”证明△AOB≌△COD还需( )| A. | AB=CD | B. | OB=OD | C. | ∠A=∠C | D. | ∠AOB=∠COD |
18. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )| A. | 小于0 | B. | 等于0 | C. | 大于0 | D. | 不能确定 |
15.下列计算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | $\sqrt{9}+\sqrt{4}=\sqrt{5}$ | C. | $\sqrt{8}+\sqrt{2}=3\sqrt{2}$ | D. | $\sqrt{{{({-5})}^2}}=-5$ |
19.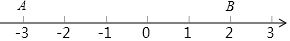 如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )
如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )
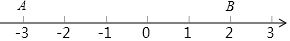 如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )
如图,A、B是数轴上两点.在线段AB上任取一点C,则点C到表示0的点的距离不大于2的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
20.不等式组$\left\{\begin{array}{l}{x-\frac{1}{2}>0}\\{1-2x≤3}\end{array}\right.$的解集为( )
| A. | x$>\frac{1}{2}$ | B. | x<-1 | C. | -1<x<$\frac{1}{2}$ | D. | x$>\frac{1}{2}$ |
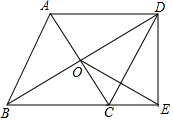 如图,菱形ABCD的对角线相交于点O,DE⊥BC的延长线于点E,若菱形的周长为20,AC=6,则线段OE的长是4.
如图,菱形ABCD的对角线相交于点O,DE⊥BC的延长线于点E,若菱形的周长为20,AC=6,则线段OE的长是4.