题目内容
等腰三角形的两边长分别为5和11,则这个三角形的周长为( )
| A、16 | B、21 |
| C、27 | D、21或27 |
考点:等腰三角形的性质,三角形三边关系
专题:分类讨论
分析:根据①11是腰长时,三角形的三边分别为11、11、5,②11是底边时,三角形的三边分别为11、5、5,分别计算即可.
解答:解:①11是腰长时,
三角形的三边分别为11、11、5,能组成三角形,
周长=11+11+5=27;
②11是底边时,
三角形的三边分别为11、5、5,
∵5+5=10<11,
∴不能组成三角形,
综上所述,三角形的周长为27.
故选C.
三角形的三边分别为11、11、5,能组成三角形,
周长=11+11+5=27;
②11是底边时,
三角形的三边分别为11、5、5,
∵5+5=10<11,
∴不能组成三角形,
综上所述,三角形的周长为27.
故选C.
点评:本题考查了等腰三角形两腰长相等的性质,要分情况讨论并利用三角形的三边关系判断是否能组成三角形.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
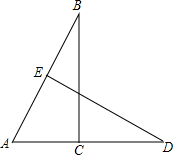 如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )
如图所示,BC⊥AD,垂足为C,∠B=∠D,则∠AED与∠BED的关系是( )| A、∠AED>∠BED |
| B、∠AED<∠BED |
| C、∠AED=∠BED |
| D、无法确定 |
矩形、菱形都具有的性质是( )
| A、对角线相等 |
| B、每一条对角线平分一组对角 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
估计
-1的值( )
| 11 |
| A、在2到3之间 |
| B、在3到4之间 |
| C、在4到5之间 |
| D、在5到6之间 |
在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,则下列条件中不能判断是直角三角形的是( )
| A、∠A=∠B-∠C |
| B、∠A:∠B:∠C=1:1:2 |
| C、a:b:c=4:5:6 |
| D、a2-c2=b2 |
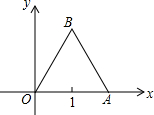 如图,已知等边三角形OAB的边长为2,求三个顶点的坐标.
如图,已知等边三角形OAB的边长为2,求三个顶点的坐标. 如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标.
如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标. 如图,∠MON=60°,点A是ON上一定点,点P是OM上一个动点(不与点O重合). 设∠OAP=x°,∠OPA=y°.
如图,∠MON=60°,点A是ON上一定点,点P是OM上一个动点(不与点O重合). 设∠OAP=x°,∠OPA=y°. 如图,一只箱子沿着斜面向上运动,箱高AB=1.2m.当BC=2.4m时,点B离地面的距离BE=1.4m,求此时点A离地面的距离(精确的0.1m).
如图,一只箱子沿着斜面向上运动,箱高AB=1.2m.当BC=2.4m时,点B离地面的距离BE=1.4m,求此时点A离地面的距离(精确的0.1m).