题目内容
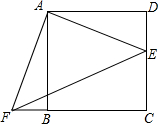
 如图,一只箱子沿着斜面向上运动,箱高AB=1.2m.当BC=2.4m时,点B离地面的距离BE=1.4m,求此时点A离地面的距离(精确的0.1m).
如图,一只箱子沿着斜面向上运动,箱高AB=1.2m.当BC=2.4m时,点B离地面的距离BE=1.4m,求此时点A离地面的距离(精确的0.1m).考点:相似三角形的应用
专题:
分析:利用相似三角形的判定与性质进而求出DF,AF的长即可得出AD的长.
解答:解:由题意可得:AD∥EB,则∠CFD=∠AFB=∠CBE,△CDF∽△CEB,
∵∠ABF=∠CEB=90°,∠AFB=∠CBE,
∴△CBE∽△AFB,
∴
=
=
,
∵BC=2.4m,BE=1.4m,
∴EC≈1.95(m),
即
=
=
,
解得:FB≈0.86,AF≈1.48,
∵△CDF∽△CEB,
∴
=
即
=
,
解得:DF≈0.9,
故AD=AF+DF=0.9+1.48≈2.4(m),
答:此时点A离地面的距离为2.4m.
∵∠ABF=∠CEB=90°,∠AFB=∠CBE,
∴△CBE∽△AFB,
∴
| BE |
| FB |
| BC |
| AF |
| EC |
| AB |
∵BC=2.4m,BE=1.4m,

∴EC≈1.95(m),
即
| 1.4 |
| FB |
| 2.4 |
| AF |
| 1.95 |
| 1.2 |
解得:FB≈0.86,AF≈1.48,
∵△CDF∽△CEB,
∴
| DF |
| BE |
| CF |
| CB |
即
| DF |
| 1.4 |
| 2.4-0.86 |
| 2.4 |
解得:DF≈0.9,
故AD=AF+DF=0.9+1.48≈2.4(m),
答:此时点A离地面的距离为2.4m.
点评:此题主要考查了相似三角形的应用,正确利用相似三角形的性质得出FD的长是解题关键.

练习册系列答案
相关题目
等腰三角形的两边长分别为5和11,则这个三角形的周长为( )
| A、16 | B、21 |
| C、27 | D、21或27 |
已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,则△ABC的腰和底边长分别为( )
| A、24cm和12cm |
| B、16cm和22cm |
| C、20cm和16cm |
| D、22cm和16cm |
下列运算正确的是( )
A、
| ||
B、(-
| ||
| C、x6÷x3=x2 | ||
| D、(x3)2=x5 |
 如图,小明把一正方形纸片分成16个全等的小正方形,并将其中四个小正方形涂成灰色.若再将一小正方形涂成灰色,使灰色区域成为轴对称图形,则此小正方形的位置在( )
如图,小明把一正方形纸片分成16个全等的小正方形,并将其中四个小正方形涂成灰色.若再将一小正方形涂成灰色,使灰色区域成为轴对称图形,则此小正方形的位置在( )| A、第一行第四列 |
| B、第二行第一列 |
| C、第三行第三列 |
| D、第四行第一列 |
 如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 如图所示,已知一个圆柱体的高为6,直径为
如图所示,已知一个圆柱体的高为6,直径为 如图,绐正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为l的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2012次“移位”后,则他所处顶点的编号是
如图,绐正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为l的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2012次“移位”后,则他所处顶点的编号是