题目内容
19.已知:a=$\frac{1}{2}$+m,b=$\frac{1}{2}$+2m,c=$\frac{1}{2}$+3m,则a2+2ab+b2-2ac+c2-2bc的值是$\frac{1}{4}$.分析 根据完全平方公式得出a2+2ab+b2-2ac+c2-2bc=(a+b-c)2=($\frac{1}{2}$+m+$\frac{1}{2}$+2m-$\frac{1}{2}$-3m)2,将a=$\frac{1}{2}$+m,b=$\frac{1}{2}$+2m,c=$\frac{1}{2}$+3m代入,计算即可求解.
解答 解:∵a=$\frac{1}{2}$+m,b=$\frac{1}{2}$+2m,c=$\frac{1}{2}$+3m,
∴a2+2ab+b2-2ac+c2-2bc=(a+b-c)2
=($\frac{1}{2}$+m+$\frac{1}{2}$+2m-$\frac{1}{2}$-3m)2
=($\frac{1}{2}$)2
=$\frac{1}{4}$.
故答案为$\frac{1}{4}$.
点评 本题考查了因式分解在求代数式值中的应用.因式分解是研究代数式的基础,通过因式分解将多项式合理变形,是求代数式值的常用解题方法,具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.如果规定符号“?”的意义为a?b=$\frac{a×b}{a+b}$,则2?(-3)的值是( )
| A. | 6 | B. | -6 | C. | $\frac{6}{5}$ | D. | $-\frac{6}{5}$ |
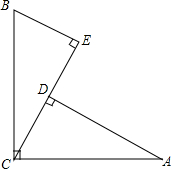 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证:
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证: 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.
如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.