题目内容
14.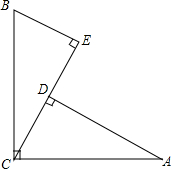 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证:
如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.求证:(1)△ACD≌△CBE;
(2)AD=BE+DE.
分析 (1)根据垂直的定义可得∠ADC=∠E=90°,然后根据同角的余角相等求出∠B=∠ACD,再利用“角角边”证明△BCE和△CAD全等;
(2)根据全等三角形对应边相等即可得证.
解答 证明:∵AD⊥CE,BE⊥CE,
∴∠ADC=∠E=90°,
∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
∵∠B+∠BCE=90°,
∴∠B=∠ACD,
在△BEC和△CDA中,
$\left\{\begin{array}{l}{∠ADC=∠E}\\{∠ACD=∠B}\\{AC=BC}\end{array}\right.$
∴△ACD≌△CBE(AAS).
(2)∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵CE=CD+DE,
∴AD=BE+DE.
点评 本题考查了全等三角形的判定与性质,根据同角的余角相等求出∠B=∠ACD是证明三角形全等的关键.

练习册系列答案
相关题目
19.已知:a=$\frac{1}{2}$+m,b=$\frac{1}{2}$+2m,c=$\frac{1}{2}$+3m,则a2+2ab+b2-2ac+c2-2bc的值是$\frac{1}{4}$.
6. 如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
(1)求证:BD=CE;
(2)连接BC,AO,并延长AO交BC于点F,试判断直线AF与BC的位置关系,并说明理由.
 如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.(1)求证:BD=CE;
(2)连接BC,AO,并延长AO交BC于点F,试判断直线AF与BC的位置关系,并说明理由.
 如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.
如图,在△ABC中,DE∥AC,EF∥AB,求证:∠EFC+∠FEC+∠DEB=180°.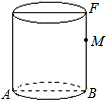 如图,已知圆柱体底面直径AB为2cm,高为4cm
如图,已知圆柱体底面直径AB为2cm,高为4cm