题目内容
11. 如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.
如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G,F分别在边AB,AC上,AH是边BC上的高,如果BC=12,AH=8,GF:BC=3:4,求矩形DEFG的周长.
分析 设EF=x,根据GF∥BC,AH⊥BC得到AK⊥GF.利用GF∥BC得到△AGF∽△ABC,然后利用相似三角形对应边成比例得到比例式即可求得x的值,进而求得矩形的周长.
解答 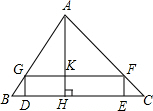 解:设EF=x,
解:设EF=x,
∵GF∥BC,AH⊥BC,
∴AK⊥GF,
∵GF∥BC,
∴△AGF∽△ABC,
∴$\frac{AK}{AH}=\frac{GF}{BC}$,
∵AH=8,BC=12,GF:BC=3:4,
∴$\frac{8-x}{8}=\frac{3}{4}$,
解得x=2,
∴DG=EF=2,GF=DE=12,
∴矩形DEFG的周长为28.
点评 本题考查了相似三角形的判定和性质、矩形的性质、矩形的周长公式,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
19.已知:a=$\frac{1}{2}$+m,b=$\frac{1}{2}$+2m,c=$\frac{1}{2}$+3m,则a2+2ab+b2-2ac+c2-2bc的值是$\frac{1}{4}$.
6. 如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
(1)求证:BD=CE;
(2)连接BC,AO,并延长AO交BC于点F,试判断直线AF与BC的位置关系,并说明理由.
 如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.
如图,AB=AC,CD⊥AB.BE⊥AC,垂足分别为D、E,BE与CD相交于点O.(1)求证:BD=CE;
(2)连接BC,AO,并延长AO交BC于点F,试判断直线AF与BC的位置关系,并说明理由.

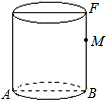 如图,已知圆柱体底面直径AB为2cm,高为4cm
如图,已知圆柱体底面直径AB为2cm,高为4cm 