题目内容
有一个运算程序:当x※y=m时(m为常数),得(x+1)※y=m+2,x※(1+y)=m-1,现在已知4※5=10,那么2014※2015= .
考点:规律型:数字的变化类
专题:新定义
分析:根据题中的新定义(x+1)※y=m+2;x※(y+1)=m-1,总结规律得:(x+N)※(y+N)=m+N(N为正整数),由4※5=10得到x=4,y=5,m=10,令N=2014,即可求出所求式子的值.
解答:解:∵(x+1)※y=m+2;x※(y+1)=m-1,
∴(x+1)※(y+1)=m+2-1=m+1,
总结规律得:(x+N)☆(y+N)=m+N(N为正整数),
由题意得:4※5=10,x=4,y=5,m=10,
N=2015可得2014※2015=10+2015=2025.
故答案为:2025.
∴(x+1)※(y+1)=m+2-1=m+1,
总结规律得:(x+N)☆(y+N)=m+N(N为正整数),
由题意得:4※5=10,x=4,y=5,m=10,
N=2015可得2014※2015=10+2015=2025.
故答案为:2025.
点评:此题考查了数字的变化规律,解决此类的探究性问题,关键是在观察、分析已知数据,寻找它们之间的相互关系,探寻其规律,关键是分析得出数字的运算规律

练习册系列答案
相关题目
 如图是一个正方体沿某些棱剪开后得到的展开图,则原正方体中“你”字一面相对面上的字是( )
如图是一个正方体沿某些棱剪开后得到的展开图,则原正方体中“你”字一面相对面上的字是( )| A、我 | B、中 | C、国 | D、梦 |
 如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )
如图,将四棱锥沿某些棱剪开,展成一个平面图形,至少需要剪开( )| A、4条棱 | B、5条棱 |
| C、6条棱 | D、7条棱 |
 如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,若MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A、AM=CN |
| B、AM∥CN |
| C、AB=CD |
| D、∠M=∠N |
小强家有两块三角形的菜地,他想判断这两块三角形菜地的形状大小是否完全一样,他设想了如下四种方法,下列方法中,不一定能判断两个三角形全等的是( )
| A、测量三边对应相等 |
| B、测量两角及其夹边对应相等 |
| C、测量两边及除夹角外的另一角对应相等 |
| D、测量两边及其夹角对应相等 |
对于有理数x,y,代数式x2+y2-xy-x+2y的最小值是( )
| A、1 | B、0 | C、-1 | D、-2 |
 如图,OA=OC,请你添加一个条件:
如图,OA=OC,请你添加一个条件: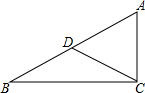 如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.
如图,∠ACB=90°,∠ADC=2∠B,AC=4,CD=3,求tan∠B.