题目内容
20.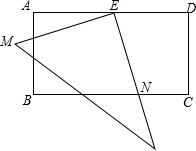 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
分析 作辅助线EF⊥BC于点F,然后证明Rt△AME≌Rt△FNE,从而求出AM=FN,所以BM与CN的长度相等.
解答  解:BM与CN的长度相等.
解:BM与CN的长度相等.
证明:在矩形ABCD中,AD=2AB,E是AD的中点,
如图,作EF⊥BC于点F,则有AB=AE=EF=FC,
∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,
∴∠AEM=∠FEN,
在Rt△AME和Rt△FNE中,
$\left\{\begin{array}{l}{∠AEM=∠FEN}\\{AE=EF}\\{∠MAE=∠NFE}\end{array}\right.$,
∴Rt△AME≌Rt△FNE,
∴AM=FN,
∴MB=CN.
点评 本题主要考查了全等三角形的判定,本题的关键是证明Rt△AME≌Rt△FNE,利用全等的性质和等量代换求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.“比a的2倍小3的数”,用代数式表示为( )
| A. | 2a+3 | B. | 2a-3 | C. | 2(a+3) | D. | 2(a-3) |
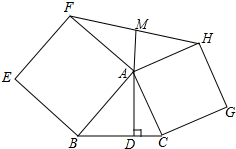 如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.
如图,分别以△ABC的边AB,AC为一边在三角形外作正方形ABEF和ACGH,M为FH上的中点,求证:MA⊥BC.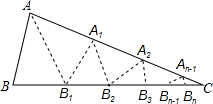 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.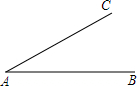 如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.
如图,线段AB和射线AC交于点A,∠A=30°,AB=20.点D在射线AC上,且∠ADB是钝角,写出一个满足条件的AD的长度值:AD=10.