题目内容
5.已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.(1)求k的值;
(2)当此方程有一根为零时,直线y=x+2与关于x的二次函数y=x2+2x+$\frac{k-1}{2}$的图象交于A、B两点,若M是线段AB上的一个动点,过点M作MN⊥x轴,交二次函数的图象于点N,求线段MN的最大值.
分析 (1)根据判别式的意义得到△=22-4×$\frac{k-1}{2}$>0,然后解不等式得到k的范围,再在k的取值范围内找出正整数即可;
(2)先把x=0代入x2+2x+$\frac{k-1}{2}$=0中求出k=-1,从而得到二次函数解析式为y=x2+2x,根据二次函数图象上点的坐标特征,设M(t,t+2)(-2<t<1),则N(t,t2+2t),所以MN可表示为t2-t+2,然后根据二次函数的性质求解.
解答 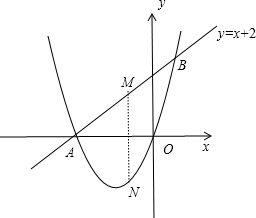 解:(1)根据题意得△=22-4×$\frac{k-1}{2}$>0,解得k<3,
解:(1)根据题意得△=22-4×$\frac{k-1}{2}$>0,解得k<3,
而k为正整数,
所以k=1或2;
(2)当x=0代入x2+2x+$\frac{k-1}{2}$=0得k=1,则方程为x2+2x=0,
二次函数为y=x2+2x,
解方程组$\left\{\begin{array}{l}{y={x}^{2}+2x}\\{y=x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,则A(-2,0),B(1,3),如图,
设M(t,t+2)(-2<t<1),则N(t,t2+2t),
所以MN=t+2-(t2+2t)=-t2-t+2=-(t+$\frac{1}{2}$)2+$\frac{9}{4}$,
当t=-$\frac{1}{2}$时,MN有最大值,最大值为$\frac{9}{4}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征和二次函数的性质;理解根的判别式的意义和一元二次方程根的定义;会通过解方程组求一次函数与二次函数图象的交点坐标.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案| A. | (2,-3) | B. | (3,2) | C. | (3,-2) | D. | (-3,-2) |
| A. | -$\frac{2}{m+3}$ | B. | $\frac{2}{m+3}$ | C. | -$\frac{2}{m-3}$ | D. | $\frac{2}{m-3}$ |

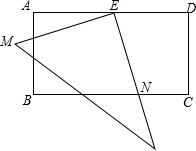 在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.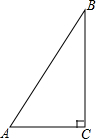 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值.
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值.