题目内容
7.阅读下面问题:$\frac{1}{1+\sqrt{2}}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2.
(1)求$\frac{1}{\sqrt{7}+\sqrt{6}}$的值;
(2)计算:$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{98}+\sqrt{99}}$+$\frac{1}{\sqrt{99}+\sqrt{100}}$.
分析 (1)原式根据阅读材料中的方法变形即可得到结果;
(2)原式各项变形后,抵消合并即可得到结果.
解答 解:(1)原式=$\frac{\sqrt{7}-\sqrt{6}}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$;
(2)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{99}$-$\sqrt{98}$+$\sqrt{100}$-$\sqrt{99}$=10-1=9.
点评 此题考查了分母有理化,弄清分母有理化的方法是解本题的关键.

练习册系列答案
相关题目
19.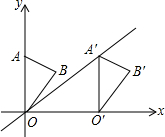 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )| A. | $\frac{2}{3}$ | B. | $\frac{9}{2}$ | C. | 3 | D. | 5 |
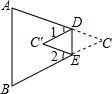 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.
如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为40°.