题目内容
15.公园要修建一个圆形喷水池,在池中心竖直安装一根水管,且在顶端安一个喷水头,使喷出的抛物线形水柱与池中心的水平距离为$\frac{3}{2}$米处达到最高,高度为$\frac{9}{4}$米,水柱落地处离池中心3米,求水管的长度.并画出函数的图象.分析 以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系,设抛物线的解析式为y=a(x-$\frac{3}{2}$)2+$\frac{9}{4}$,将(3,0)代入求得a值,x=0时得到的y值即为水管的长.
解答  解:以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
解:以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
代入(3,0)求得:a=-1,
∴y=-(x-$\frac{3}{2}$)2+$\frac{9}{4}$,
令x=0,则y=0.
故水管长为0m.
点评 本题考查了二次函数在实际生活中的运用,重点是二次函数解析式的求法,利用顶点式求出解析式是解题关键.

练习册系列答案
相关题目
6.小张上周五在股市以收盘价每股25元买进某公司的股票1000股,在接下来的一周交易日内,小王记下该股票每日收盘价格相比前一天的涨跌情况如下(单位:元):
根据上表回答问题:
(1)星期二收盘时,该股票每股是多少元?
(2)这周内该股票收盘时的最高价、最低价分别在星期几?各是多少元?
(3)已知买入股票与卖出股票均需支付成交金额的千分之二交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨(元) | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
(1)星期二收盘时,该股票每股是多少元?
(2)这周内该股票收盘时的最高价、最低价分别在星期几?各是多少元?
(3)已知买入股票与卖出股票均需支付成交金额的千分之二交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
10.掷一颗均匀的骰子(正方体,各面标1-6这6个数字),6点朝上的概率为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{6}$ |
4.求作点P,使P到三角形三边的距离相等的方法是( )
| A. | 作两边的中垂线的交点 | B. | 作两边上的高线的交点 | ||
| C. | 作两边上的中线的交点 | D. | 作两角平分线的交点 |
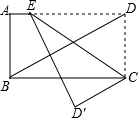 如图,将一张矩形纸片ABCD沿CE折叠,使D点落在D′点处,若CD′∥DB,∠ABD=66°,则∠DCE的度数为57°.
如图,将一张矩形纸片ABCD沿CE折叠,使D点落在D′点处,若CD′∥DB,∠ABD=66°,则∠DCE的度数为57°.