题目内容
19.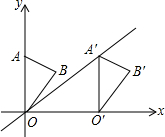 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=$\frac{2}{3}$x上一点,则点B与其对应点B′间的距离为( )| A. | $\frac{2}{3}$ | B. | $\frac{9}{2}$ | C. | 3 | D. | 5 |
分析 根据平移的性质知BB′=AA′.由一次函数图象上点的坐标特征可以求得点A′的坐标,所以根据两点间的距离公式可以求得线段AA′的长度,即BB′的长度.
解答 解:如图,连接AA′、BB′. ∵点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,
∵点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,
∴点A′的纵坐标是3.
又∵点A′在直线y=$\frac{2}{3}$x上一点,
∴3=$\frac{2}{3}$x,解得x=$\frac{9}{2}$.
∴点A′的坐标是($\frac{9}{2}$,3),
∴AA′=$\frac{9}{2}$.
∴根据平移的性质知BB′=AA′=$\frac{9}{2}$.
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
10.掷一颗均匀的骰子(正方体,各面标1-6这6个数字),6点朝上的概率为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{6}$ |
14.若一次函数y=kx的图象经过(3,2),则k的值为( )
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | $\frac{2}{3}$ |
4.求作点P,使P到三角形三边的距离相等的方法是( )
| A. | 作两边的中垂线的交点 | B. | 作两边上的高线的交点 | ||
| C. | 作两边上的中线的交点 | D. | 作两角平分线的交点 |
8.若方程(x-3)2+a=0有实数根,则a的取值范围是( )
| A. | a≤0 | B. | a≥0 | C. | a≠0 | D. | a为任意实数 |
6.在Rt△ABC中,AD是斜边BC上的高,若CB=a,∠B=β,则AD等于( )
| A. | asin2β | B. | acos2β | C. | asinβcosβ | D. | asinβtanββ |
 如图,已知△ABD≌△CDB,且∠ABD=40°,∠CBD=20°,则∠A的度数为120°.
如图,已知△ABD≌△CDB,且∠ABD=40°,∠CBD=20°,则∠A的度数为120°.