题目内容
11.矩形具有而平行四边形不一定具有的性质是( )| A. | 对角线互相平分 | B. | 两组对角相等 | C. | 对角线相等 | D. | 两组对边相等 |
分析 根据矩形、平行四边形的性质一一判断即可解决问题.
解答 解:A、错误.对角线互相平分,矩形、平行四边形都具有的性质.
B、错误.两组对角相等,矩形、平行四边形都具有的性质.
C、正确.对角线相等,矩形具有而平行四边形不一定具有.
D、错误.两组对边相等,矩形、平行四边形都具有的性质.
故选C.
点评 本题考查矩形的性质、平行四边形的性质,解题的关键是熟练掌握平行四边形、矩形的性质,属于中考常考题型.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
1. 某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
结合图表完成下列问题:
(1)a=2;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀的学生人数占全班总人数的百分之几?
 某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:| 次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
| 频数 | a | 4 | 12 | 16 | 8 | 3 |
(1)a=2;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀的学生人数占全班总人数的百分之几?
2.函数$y=\frac{1}{x-2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x≥2 | D. | x=2 |
3.点P(-2,3)关于y轴的对称点的坐标是( )
| A. | (2,3 ) | B. | (-2,-3) | C. | (-2,3) | D. | (-3,2) |
20.△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{2}+1$ |
2. 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
 如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )
如图,△ABC和△DBE中,AB=CB,DB=EB,∠ABC=∠DBE=50°.若∠BDC=25°,AD=4,DE=$\sqrt{13}$,则CD的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | 2 |
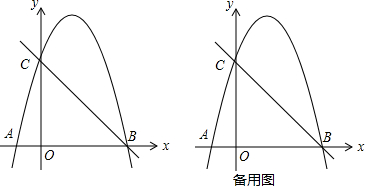 如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)
如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)