题目内容
10.某电信公司给顾客提供上网费有两种计算方式,方式A以每分钟0.1元的价格按上网的时间计费;方式B除收月基费20元外再以每分钟0.05元的价格按上网时间计费,设上网时间为x分钟,所需费用为y元.(1)分别按方式A、方式B收费时,y与x的函数关系式;
(2)当每月上网时间为500分钟时,选择哪种收费方式比较划算.
分析 (1)根据“费用=每分钟费用×通话时间”可得出yA关于x的函数关系式,再根据“费用=每分钟费用×通话时间+月基费”即可得出yB关于x的函数关系式;
(2)将x=500分别代入(1)中的两个函数关系式中,求出yA和yB,再进行比较即可得出结论.
解答 解:(1)由题意得:yA=0.1x;
yB=0.05x+20.
(2)当x=500时,yA=0.1×500=50;
当x=500时,yB=0.05×500+20=45.
∵50>45,
∴当每月上网时间为500分钟时,选择收费方式B比较划算.
点评 本题考查了一次函数的应用,解题的关键是:(1)根据数量关系找出函数关系式;(2)代入x的值求出y值.本题属于基础题,难度不大,解决该题型题目时,根据数量关系找出函数关系式是关键.

练习册系列答案
相关题目
20.已知点A(a+3,4-a)在y轴上,则点A的坐标为( )
| A. | (0,1) | B. | (0,7) | C. | (0,-7) | D. | (7,0) |
1. 某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
结合图表完成下列问题:
(1)a=2;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀的学生人数占全班总人数的百分之几?
 某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:
某校七年(1)班体育委员统计了全班同学60秒跳绳的次数,并绘制出频数分布表和频数分布直方图:| 次数 | 80≤x<100 | 100≤x<120 | 120≤x<140 | 140≤x<160 | 160≤x<180 | 180≤x<200 |
| 频数 | a | 4 | 12 | 16 | 8 | 3 |
(1)a=2;
(2)补全频数分布直方图;
(3)若跳绳次数不少于140的学生成绩为优秀,则优秀的学生人数占全班总人数的百分之几?
18.下列调查中,适宜采用全面调查方式的是( )
| A. | 调查某品牌钢笔的使用寿命 | |
| B. | 了解某市学生的视力情况 | |
| C. | 调查乘坐飞机的乘客是否携带违禁物品 | |
| D. | 了解某市学生课外阅读情况 |
5. 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 0.450 | |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | ||
| 1600~1799 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
(2)频数分布直方图的组距是多少?这个组距选择得好不好?请判断并说明理由.
(3)如果家庭人均月收入“大于999不足1600元”的为中等收入家庭,请你通过样本估计总体中的中等收入家庭大约有多少户?
2.函数$y=\frac{1}{x-2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x≥2 | D. | x=2 |
20.△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{2}+1$ |
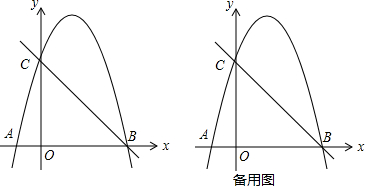 如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)
如图,已知抛物线y=ax2-3ax-4a(a≠0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,∠ACB=90°,点D 的坐标为(0,3)