题目内容
13.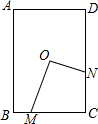 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
分析 求两条线段的关系,把两条线段放到两个三角形中,利用两个三角形的关系求解.
解答 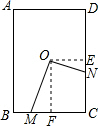 解:如图,作OF⊥BC于F,OE⊥CD于E,
解:如图,作OF⊥BC于F,OE⊥CD于E,
∵四边形ABCD为矩形,
∴∠C=90°,
∵OF⊥BC,OE⊥CD,
∴∠EOF=90°,
∴∠EON+∠FON=90°,
∵ON⊥OM,
∴∠EON=∠FOM,
∴△OEN∽△OFM,
∴$\frac{OE}{OF}=\frac{ON}{OM}$,
∵O为矩形ABCD的中心,
∴$\frac{OF}{OE}=\frac{AB}{AD}=\frac{6}{4}=\frac{3}{2}$,
∴$\frac{OM}{ON}=\frac{3}{2}$,
即y=$\frac{2}{3}$x.
故选D.
点评 此题主要考查的是相似三角形的判定与性质,解题的关键是合理的在图中作出辅助线,熟练掌握相似三角形的判定定理和性质是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
7.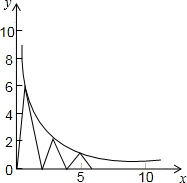 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
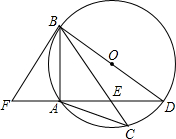 如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.
如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC. 如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.
如图是由五块积木搭成的,这几块积木都是相同的正方体,请你画出从这个图形的正面看、上面看、左面看的平面图.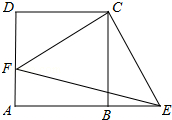 如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.
如图,正方形ABCD中,点F在AD上,点E在AB的延长线上,∠FCE=90°.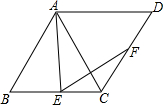 如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.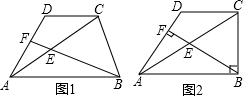 如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.
如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.