题目内容
8.当x=$\frac{1}{2}$时,$\frac{1}{x-2}$与$\frac{1}{x+1}$互为相反数.分析 利用互为相反数两数之和为0列出方程,求出方程的解即可得到结果.
解答 解:根据题意得:$\frac{1}{x-2}$+$\frac{1}{x+1}$=0,
去分母得:x+1+x-2=0,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解.
故答案为:$\frac{1}{2}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
13.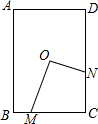 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
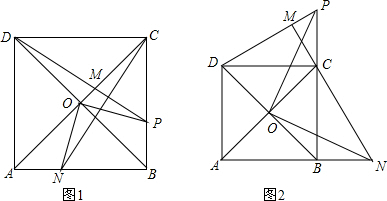 在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示.
在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示.
 如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.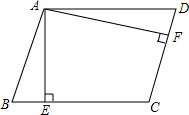 如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长.
如图所示,?ABCD的相邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=4cm,求AF的长. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$. 配方后所得的方程是
配方后所得的方程是 B.
B.  C.
C.  D.
D. 