题目内容
2.若分式$\frac{|a|}{a-{a}^{2}}$=$\frac{1}{a-1}$,求a的取值范围.分析 根据分式的基本性质,可得答案.
解答 解:由分式$\frac{|a|}{a-{a}^{2}}$=$\frac{1}{a-1}$,得
a<0.
点评 本题考查了分式基本性质,分式的分子分母都乘以或除以同一个不为零的数或者,分式的值不变.

练习册系列答案
相关题目
13.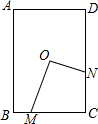 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
10.一元二次方程x2-6x+8=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
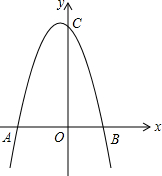 如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C. ____________
____________ B.
B.  C.
C.  D.
D. 
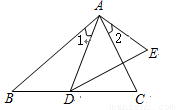
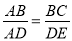 B.
B. 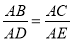 C. ∠B=∠ADE D. ∠C=∠E
C. ∠B=∠ADE D. ∠C=∠E