题目内容
5.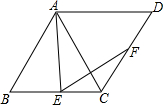 如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
分析 作EG∥AB于G,则∠GEC=∠B=60°,先证明△ABC是等边三角形,∠BCF=120°,得出∠ACB=60°,再证明△GEC是等边三角形,得出EG=EC,∠EGC=60°,得出∠EAG=120°,证出∠1=∠2,由ASA证明△AEG≌△FEC,得出对应边相等即可.
解答 解:作EG∥AB于G,如图所示: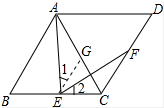 则∠GEC=∠B=60°,
则∠GEC=∠B=60°,
∵四边形ABCD是菱形,
∴AB=BC=CD=DA,∠D=∠B=60°,∠ACB=∠ACD,
∴△ABC是等边三角形,∠BCF=120°,
∴∠ACB=60°,
∴∠ACB=∠GEC=60°,
∴△GEC是等边三角形,
∴EG=EC,∠EGC=60°,
∴∠EAG=120°,
∵∠AEF=60°=∠GEC,
∴∠1=∠2,
在△AEG和△FEC中,
$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{EG=EC}&{\;}\\{∠EGA=∠ECF=120°}&{\;}\end{array}\right.$,
∴△AEG≌△FEC(ASA),
∴AE=EF.
点评 本题考查了菱形的性质、等边三角形的判定与性质、全等三角形的判定与性质;熟练掌握菱形的性质,证明三角形全等和等边三角形是解决问题的关键.

练习册系列答案
相关题目
13.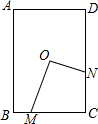 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
 (1)三角形的内角和等于180°;
(1)三角形的内角和等于180°; 如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是3,S3的值为$\frac{81}{8}$. B.
B.  C.
C.  D.
D. 
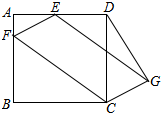 如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.
如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.