题目内容
7.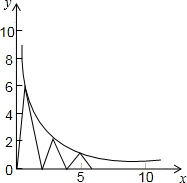 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
分析 分别求出第1个、第2个、第3个、第4个三角形底边上的高,找出规律即可得出结论.
解答 解:∵每个等腰三角形的底边长为2,顶点在反比例函数y=$\frac{6}{x}$的图象上,
∴第1个三角形底边上的高=$\frac{6}{1}$=$\frac{6}{2×1-1}$;
第2个三角形底边上的高=$\frac{6}{3}$=$\frac{6}{2×2-1}$;
第3个三角形底边上的高=$\frac{6}{5}$=$\frac{6}{2×3-1}$;
第4个三角形底边上的高=$\frac{6}{7}$=$\frac{6}{2×4-1}$;
…;
∴第n个三角形底边上的高=$\frac{6}{2n-1}$.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
20.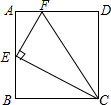 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;④若$\frac{BC}{CD}$=$\frac{\sqrt{3}}{2}$,则△CEF≌△CDF.
 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;④若$\frac{BC}{CD}$=$\frac{\sqrt{3}}{2}$,则△CEF≌△CDF.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
13.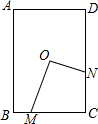 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
 (1)三角形的内角和等于180°;
(1)三角形的内角和等于180°;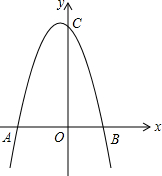 如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
 如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D.
如图,已知BD为∠ABC的平分线,CD为△ABC的外角∠ACE的平分线,CD与BD交于点D,试说明∠A=2∠D. B.
B.  C.
C.  D.
D. 