题目内容
9.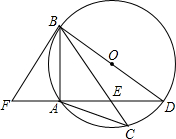 如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.
如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.(1)求证:BF是⊙O的切线;
(2)若AD=8,tan∠ABF=$\frac{3}{4}$,求DE的长.
分析 (1)根据圆周角定理得出∠BAD=90°,进而得出∠D+∠DBA=90°.根据AB=AC,得出∠CBA=∠D,进而得出∠D=∠ABF,从而得出∠ABF+∠DBA=90°,即OB⊥BF,即可证得BF为⊙O的切线;
(2)由tan∠ABF=$\frac{3}{4}$,得出tan∠D=$\frac{AB}{AD}$=$\frac{3}{4}$,得出AB=6,进而根据tan∠ABC=$\frac{AE}{AB}$=$\frac{3}{4}$,即可求得AE,进而求得DE.
解答 解:(1)∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠D+∠DBA=90°.
∵AB=AC,
∴∠CBA=∠D,
又∵∠ABF=∠ABC,
∴∠D=∠ABF,
∴∠ABF+∠DBA=90°,
即OB⊥BF,
∴BF为⊙O的切线;
(2)由(1)知,∠D=∠ABF,
∴tan∠D=$\frac{AB}{AD}$=$\frac{3}{4}$,
∴AB=$\frac{3}{4}$×8=6,
∵∠ABC=∠ABF,
∴tan∠ABC=$\frac{AE}{AB}$=$\frac{3}{4}$,
∴AE=$\frac{9}{2}$.
DE=AD-AE=8-$\frac{9}{2}$=$\frac{7}{2}$.
点评 此题考查了切线的判定以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
20.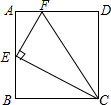 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;④若$\frac{BC}{CD}$=$\frac{\sqrt{3}}{2}$,则△CEF≌△CDF.
 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论正确的是( )①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;④若$\frac{BC}{CD}$=$\frac{\sqrt{3}}{2}$,则△CEF≌△CDF.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
17.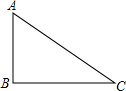 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )| A. | $2\sqrt{5}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
13.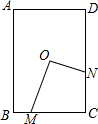 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
 如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )
如图,D为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为( )| A. | $y=\frac{1}{2}x$ | B. | $y=\frac{1}{3}x$ | C. | $y=\frac{1}{2}x$+2 | D. | $y=\frac{2}{3}x$ |
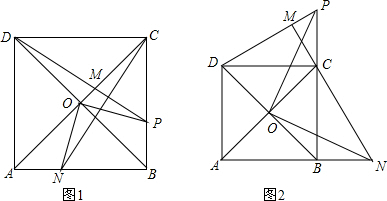 在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示.
在边长为4的正方形ABCD中,点O是正方形对角线的交点,动点P在射线BC上运动,过点C作线段DP的垂线,交线段DP于点M,交直线AB于点N,连结OP,ON.当点P在线段BC上运动时,如图1所示;当点P在线段BC的延长线上运动时,如图2所示. (1)三角形的内角和等于180°;
(1)三角形的内角和等于180°;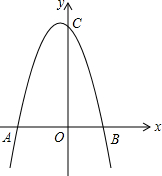 如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.