题目内容
 如图,AB是⊙O的直径,切线PC与AB延长线交于C,P为切点,点D是
如图,AB是⊙O的直径,切线PC与AB延长线交于C,P为切点,点D是 |
| AP |
(1)求证:DO∥BP;
(2)求⊙O的半径.
考点:切线的性质
专题:计算题
分析:(1)由点D是
的中点,即
=
,则根据垂径定理得OD⊥AP,再根据圆周角定理得∠APB=90°,然后根据平行线的判定即可得到DO∥BP;
(2)连结OP,如图,设⊙O的半径为r,根据切线的性质得OP⊥PC,在Rt△OPC中,由于PC=6,OC=AC-OA=r,OP=r,则根据勾股定理得(10-r)2=36+r2,然后解方程即可得到⊙的半径.
 |
| AP |
 |
| AD |
 |
| PD |
(2)连结OP,如图,设⊙O的半径为r,根据切线的性质得OP⊥PC,在Rt△OPC中,由于PC=6,OC=AC-OA=r,OP=r,则根据勾股定理得(10-r)2=36+r2,然后解方程即可得到⊙的半径.
解答:(1)证明:∵点D是
的中点,
∴
=
,
∴OD⊥AP,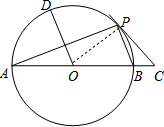
∵AB是⊙O的直径,
∴∠APB=90°,
∴PB⊥AP,
∴DO∥BP;
(2)解:连结OP,如图,设⊙O的半径为r,
∵PC是⊙O的切线,
∴OP⊥PC,
在Rt△OPC中,∵PC=6,OC=AC-OA=r,OP=r,
∴(10-r)2=36+r2,解得r=
,
即⊙O的半径为
.
 |
| AP |
∴
 |
| AD |
 |
| PD |
∴OD⊥AP,

∵AB是⊙O的直径,
∴∠APB=90°,
∴PB⊥AP,
∴DO∥BP;
(2)解:连结OP,如图,设⊙O的半径为r,
∵PC是⊙O的切线,
∴OP⊥PC,
在Rt△OPC中,∵PC=6,OC=AC-OA=r,OP=r,
∴(10-r)2=36+r2,解得r=
| 16 |
| 5 |
即⊙O的半径为
| 16 |
| 5 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了垂径定理、勾股定理和平行线的判定.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为( )
如图,在平行四边形ABCD中,AD=7,CE平分∠BCD交AD边于点E,且AE=4,则AB的长为( )| A、4 | ||
| B、3 | ||
C、
| ||
| D、2 |
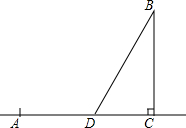 由沿河城市A运货物到离河岸30km的地点B,按沿河距离计算,B离A的沿河距离AC是40km.如果水路运费是公路运费的一半,应怎样确定在河岸上的D,从B修一条公路到D,使由A到B的运费最省?
由沿河城市A运货物到离河岸30km的地点B,按沿河距离计算,B离A的沿河距离AC是40km.如果水路运费是公路运费的一半,应怎样确定在河岸上的D,从B修一条公路到D,使由A到B的运费最省? 如图,△ABC中,∠A=30°,AC=2
如图,△ABC中,∠A=30°,AC=2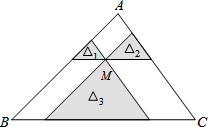 如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为
若二次函数y=-x2+bx+c的部分图象如图所示,则关于x的一元二次方程-x2+bx+c=0的一个解是x1=3,则另一个解为 如图,∠B与哪个角是内错角,与哪个角是同旁内角?被哪一条直线所截得形成的?对∠C进行同样的讨论?
如图,∠B与哪个角是内错角,与哪个角是同旁内角?被哪一条直线所截得形成的?对∠C进行同样的讨论?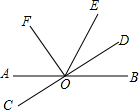 如图,直线AB,CD交于O点,OD,OF分别平分∠BOE,∠AOE.
如图,直线AB,CD交于O点,OD,OF分别平分∠BOE,∠AOE.