题目内容
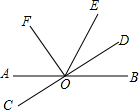 如图,直线AB,CD交于O点,OD,OF分别平分∠BOE,∠AOE.
如图,直线AB,CD交于O点,OD,OF分别平分∠BOE,∠AOE.(1)若∠AOC=36°,试分别求∠EOF,∠FOD的度数;
(2)试探索:若改变∠AOC的大小,则∠DOF得大小如何变化?说明理由.
考点:对顶角、邻补角,角平分线的定义
专题:
分析:(1)根据角平分线的性质可得∠AOF=∠FOE=
∠AOE,∠EOD=∠BOD=
∠EOB,进而可得∠FOE+∠EOD=90°;根据∠AOC=36°可得∠BOD=36°,再根据余角的性质可得∠EOF;
(2)根据角平分线的性质可得∠AOF=∠FOE=
∠AOE,∠EOD=∠BOD=
∠EOB,进而可得∠FOE+∠EOD=90°.
| 1 |
| 2 |
| 1 |
| 2 |
(2)根据角平分线的性质可得∠AOF=∠FOE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OD,OF分别平分∠BOE,∠AOE,
∴∠AOF=∠FOE=
∠AOE,∠EOD=∠BOD=
∠EOB,
∵∠AOE+∠BOE=180°,
∴∠FOE+∠EOD=90°,
∴∠FOD=90°,
∵∠AOC=36°,
∴∠BOD=36°,
∴∠DOE=36°,
∴∠EOF=90°-36°=54°;
(2)改变∠AOC的大小,则∠DOF得大小不变,
∵OD,OF分别平分∠BOE,∠AOE,
∴∠AOF=∠FOE=
∠AOE,∠EOD=∠BOD=
∠EOB,
∵∠AOE+∠BOE=180°,
∴∠FOE+∠EOD=90°.
∴∠AOF=∠FOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOE+∠BOE=180°,
∴∠FOE+∠EOD=90°,
∴∠FOD=90°,
∵∠AOC=36°,
∴∠BOD=36°,
∴∠DOE=36°,
∴∠EOF=90°-36°=54°;
(2)改变∠AOC的大小,则∠DOF得大小不变,
∵OD,OF分别平分∠BOE,∠AOE,
∴∠AOF=∠FOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOE+∠BOE=180°,
∴∠FOE+∠EOD=90°.
点评:此题主要考查了角平分线的性质,以及对顶角,关键是掌握角平分线把角分成相等的两部分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图中的同旁内的角共有( )
如图中的同旁内的角共有( )| A、1对 | B、2对 | C、3对 | D、4对 |
 如图,AB是⊙O的直径,切线PC与AB延长线交于C,P为切点,点D是
如图,AB是⊙O的直径,切线PC与AB延长线交于C,P为切点,点D是
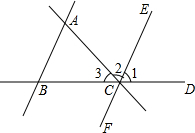 如图,直线BD上有一点C,则:
如图,直线BD上有一点C,则: 分别指出如图中的同位角、内错角、同旁内角.
分别指出如图中的同位角、内错角、同旁内角.