题目内容
如图，△ABC中，∠A=30°，AC=2| 3 |
| 3 |
（1）求点C到AB边的距离；
（2）求∠B的度数．
考点：解直角三角形
专题：
分析：（1）利用过点C作CD⊥AB于点D，结合直角三角形中30°所对的直角边等于斜边的一半，进而得出CD的长；
（2）由（1）得出BD的长，再利用等腰三角形的性质得出∠B的度数．
（2）由（1）得出BD的长，再利用等腰三角形的性质得出∠B的度数．
解答：
解：（1）如图所示：过点C作CD⊥AB于点D，
∵∠A=30°，AC=2
，
∴CD=
AC=
；
（2）由（1）得：AD=
=3，
∵AB=3+
，
∴BD=AB-AD=3+
-3=
，
∴BD=CD=
，
∴∠B=45°．
解：（1）如图所示：过点C作CD⊥AB于点D，∵∠A=30°，AC=2
| 3 |
∴CD=
| 1 |
| 2 |
| 3 |
（2）由（1）得：AD=
| AC2-CD2 |
∵AB=3+
| 3 |
∴BD=AB-AD=3+
| 3 |
| 3 |
∴BD=CD=
| 3 |
∴∠B=45°．
点评：此题主要考查了解直角三角形，正确利用勾股定理求出是解题关键．
练习册系列答案
相关题目
如图，AB是⊙O的直径，CD切⊙O于C，OD⊥AB交AC于E，tan∠DEC=3，求sin∠D的值．
请在方格纸上画出与AB、CD垂直的线段，并用字母表示．
如图，在△ABC中，DE∥BC，分别交AB，AC于点D，E．若AD=1，DB=2，则△ADE的面积与△ABC的面积的比等于（ ）A、
| ||
B、
| ||
C、
| ||
| D、1：9 |
如图，AB是⊙O的直径，切线PC与AB延长线交于C，P为切点，点D是
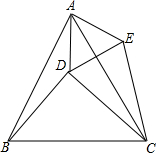如图，△ABC是等边三角形，△BDC是等腰直角三角形，∠BDC=90°，连接AD，以AD为边作等边△ADE，连接CE．
如图中的同旁内的角共有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |